LADA Priora седан – Технические характеристики – Официальный сайт LADA
Колесная формула / ведущие колеса
Расположение двигателя
Тип кузова / количество дверей
Количество мест
Длина / ширина / высота, мм
База, мм
Колея передних / задних колес, мм
Дорожный просвет, мм
Объем багажного отделения, л
Код двигателя
Тип двигателя
Система питания
Количество, расположение цилиндров
Рабочий объем, куб. см
Максимальная мощность, кВт (л.с.) / об. мин.
Максимальный крутящий момент, Нм / об. мин.
Рекомендуемое топливо
Максимальная скорость, км/ч
Время разгона 0-100 км/ч, с
Городской цикл, л/100 км
Загородный цикл, л/100 км
Смешанный цикл, л/100 км
Снаряженная масса, кг
Технически допустимая максимальная масса, кг
Максимальная масса прицепа без тормозной системы /…
Тип трансмиссии
Передаточное число главной передачи
Передняя
Задняя
Рулевой механизм
Размерность
Лада Приора – все, что нужно знать об увеличении клиренса. Часть 1
Лада Приора – все, что нужно знать об увеличении клиренса. Часть 1
Лада Приора сменила морально устаревшее семейство ВАЗ 2110, унаследовав от этих машин лучшие узлы и агрегаты. Клиренс Приоры избыточен для европейских дорог, однако на российских дорогах его хватает не везде.
Как увеличить дорожный просвет
Способов увеличить дорожный просвет Приоры несколько. Самый дешевый и худший способ – установка межвитковых проставок. В результате такого увеличения клиренса жесткость возрастает подвески, увеличивается клиренс и снижается ресурс пружин, которые ломаются через 50–80 тысяч километров.
Третий по популярности способ – установка пакета для плохих дорог. Такие пакеты изготавливают предприятия – партнеры АВТОВАЗ, поэтому вы сможете подобрать комплект, который лучше других отвечает вашим пожеланиям. Если подобрать готовый пакет не удалось, его можно набрать самостоятельно, ведь он состоит из стоек и пружин увеличенной длины, но меньшей жесткости.
Какой клиренс у приоры седан
Новая Лада Приора багажник, размеры, габариты, клиренс, дорожный просвет Lada Priora рестайлинг
Размеры рестайлинговой Лады Приоры существенно не изменились. Хотя за счет новых передних и задних бамперов длина Lada Priora изменилась на несколько миллиметров.
По прежнему седан Lada Priora рестайлинг имеет самую большую длину, которая в новой версии составляет 4 350 мм. Длина универсала на 1 сантиметр короче, а вот хэтчбек Приора еще меньше, длина этой версии кузова составляет 4210 мм. Ширина всего семейства составляет 1 680 мм и колесная база одинакова для всех 2 492 мм. А вот высота у всех разная, седан Лада Приора 1 420 мм, хэтчбек 1 435 мм, а вот универсал вообще 1 508 мм в высоту. Большая высота универсала Priora объясняется наличием рейлингов на крыше. У хэтчбека же конструкция задней части кузова такова, что автомобиль получился выше седана.
Большая высота универсала Priora объясняется наличием рейлингов на крыше. У хэтчбека же конструкция задней части кузова такова, что автомобиль получился выше седана.
Что касается дорожного просвета или клиренса Лада Приора, то производитель указывает на цифру 165 мм у седана и хэтчбека, а у универсала Lada Priora клиренс составляет 170 мм. Однако по факту дорожный просвет больше, достаточно взять в руки рулетку и убедится в этом. Но производитель не ошибается, просто указывает дорожный просвет автомобиля при полной загрузке. В то же самое время производители иномарок хитрят и указывают дорожный просвет своих автомобилей в не нагруженном состоянии. поэтому реальный дорожный просвет иномарок и их официальные данные часто не совпадают.
Объемы багажного отделения у новой версии Лада Приора во всех трех кузовах мало изменились. Объем багажника седана составляет 430 литров. Объем багажного отделения хэтчбека Priora меньше, всего 306 литров, но если сложить задние сидения (чего нельзя сделать в седане), то объем возрастает до 705 литров. В Приора универсал объем багажного отделения составляет 444 литров, а при сложенных сидениях достигает 777 литров. К сожалению задние сидения не складываются в ровень с полом, да и большие колесные арки съедают довольно много багажного пространства.
В Приора универсал объем багажного отделения составляет 444 литров, а при сложенных сидениях достигает 777 литров. К сожалению задние сидения не складываются в ровень с полом, да и большие колесные арки съедают довольно много багажного пространства.
Далее подробные данные о габаритах Лада Приора в таблице ниже.
0 0 голос
Рейтинг статьи
выгода от большого дорожного просвета
Приобретая автомобиль, покупатель должен обращать внимание на множество моментов. Так, например, нужно выбрать машину в соответствии с теми задачами, которые вы перед ней намерены ставить. Если цели ваших поездок не будут выходить за пределы города, то приобретайте малолитражку, а если вам требуется пересечь бездорожье, то обратите внимание на внедорожники с объемными двигателями.
А можно совместить и то и другое, купив малолитражный автомобиль, а затем сделав его пригодным для пересечения плохих дорог. Сотворить такую универсальную машину можно, просто увеличив дорожный просвет имеющегося у вас автомобиля. В условиях российских дорог подобные махинации всегда будут актуальными. Так, например, увеличив дорожный просвет на таком автомобиле, как «Приора», вы сэкономите немало денег на ее ремонте. Ведь вам попусту не придется чинить подвеску после встречи с парой-тройкой ям.
В условиях российских дорог подобные махинации всегда будут актуальными. Так, например, увеличив дорожный просвет на таком автомобиле, как «Приора», вы сэкономите немало денег на ее ремонте. Ведь вам попусту не придется чинить подвеску после встречи с парой-тройкой ям.
Как получить выгоду от увеличения клиренса?
Разумеется, ни удвоенный, ни утроенный дорожный просвет «Приоры» не сравнится с клиренсом любого внедорожника. Однако не стоит забывать, что, в тандеме с улучшением некоторых других характеристик машины, клиренс «Приоры» может дать неплохие результаты. Сейчас проясним.
Расстояние от земли до нижней центральной точки «Приоры» составляет 165 мм. Однако знание одного этого факта недостаточно для каких-либо выводов. Автомобилист обязательно должен учесть и указанные ниже характеристики, такие как:
- Полная длина машины.
- Расстояние от переднего свеса до заднего.
- База колес.
- Ширина колеи автомобиля.
- Наличие каких-либо деталей, выступающих под дном машины.

- То, насколько изменяется дорожный просвет, когда автомобиль полностью загружен.
Только работа над совместным улучшением всех этих характеристик может привести к получению пользы от увеличения дорожного просвета «Приоры».
Параметры кузовов «Приоры»
В любом кузове «Приоры» характеристики ее колес и колесных баз будут одинаковы, а потому указывать их везде в отдельности не имеет смысла. Вот эти самые параметры:
| Параметр | Описание | Значение |
| Колесная база | Расстояние между центрами передних и задних колес | 2492 мм |
| Колея передних колес | Расстояние между следами протекторов шин на передней оси | 1410 мм |
| Колея задних колес | Расстояние между протекторами шин задний оси | 1380 мм |
Эти габариты верны для всех кузовов, за исключением купе. Параметры хэтчбека:
Параметры хэтчбека:
- Расстояние от задней до передней точки автомобиля — 4210 мм.
- Передний свес машины — 770 мм.
- Задний свес машины — 660 мм.
- Расстояние от задней до передней точки машины — 4350 мм.
- Передний свес автомобиля — 740 мм.
- Задний свес автомобиля — 830 мм.
Параметры купе:
- Расстояние от задней до передней подвески автомобиля — 440 мм.
- База колес автомобиля — 2492 мм.
Свесы автомобилей более спортивных вариантов производителем не указаны. Учитывая, что клиренс «Приоры» составляет 165 мм, мы можем подобрать наилучший тип кузова, позволяющий использовать дорожный просвет более удачно, чем иные. Проанализировав все имеющиеся характеристики, мы обязательно придем к выводу, что вариант хэтчбек гораздо лучше всех остальных.
Габариты Лады ПриорыДостаточно большая колесная база, имеющаяся у кузова, несмотря на его маленькую длину, позволяет назвать машину обладательницей большой проходимости. Однако необходимо напомнить владельцам «Приоры» о том, что, даже будучи обладателем хэтчбека, нужно со всей осторожностью относиться к парковке рядом с высокими бордюрами. Особенно актуально это предупреждение тогда, когда ваша машина полностью загружена.
Однако необходимо напомнить владельцам «Приоры» о том, что, даже будучи обладателем хэтчбека, нужно со всей осторожностью относиться к парковке рядом с высокими бордюрами. Особенно актуально это предупреждение тогда, когда ваша машина полностью загружена.
Но если «Приору» хэтчбек с большой натяжкой можно назвать покорительницей лесных дорог и горных вершин, то кузов купе подобного титула удостоиться никак не может. У такой машины слишком уж длинное расстояние между передними и задними колесами и очень большой передний свес. Как ни крути, но по деревенским проселкам на ней проехать будет трудновато. Подобная конструкция автомобиля хороша исключительно для асфальтных покрытий.
Однако даже на них нужно будет очень аккуратно ездить там, где имеются крупные выбоины и есть необходимость преодоления искусственных неровностей. Но поскольку лишних и выступающих частей из-под трансмиссии на «Приоре» нет, вы можете с уверенностью рассчитывать на качество имеющегося дорожного просвета.
Несмотря на отсутствие торчащих из-под днища «Приоры» деталей, можно сильно уменьшить величину клиренса, если посадить в машину много людей и загрузить багажник вещами. Снижение его длины только лишь на 20 мм уже будет достаточно для касания поверхности «лежачего полицейского» днищем. Следует форсировать подобные препятствия с особой тщательностью, дабы вовремя устранить возможность появления поломок.
Способы увеличения клиренса
Надо заметить, что люди находят пользу не только в увеличении клиренса, но и в его уменьшении. Так, например, сократив дорожный просвет, автомобилисты добиваются уменьшения кренов машины направо или налево при прохождении поворотов на высокой скорости. Однако если вы не являетесь гонщиком или не имеете пристрастия к быстрой езде, то вам скорее подойдет идея увеличить клиренс.
То, как мы будем увеличивать клиренс, зависит от запланированной нами его конечной длины. При этом способы воздействия на дорожный просвет Лады будут различными, а некоторые из них повлияют на улучшение остальных характеристик автомобиля.
Установка проставок на автомобиль
Проставки — это детали, устанавливающиеся между кузовом машины и ее стойками. Они крепятся прямо на опору. Поскольку к увеличению клиренса прибегают очень многие автомобилисты, некоторые производители включают проставки прямо в комплект со стойками к машине.
Однако если вы не обнаружили их во время осмотра имеющихся заводских деталей, то не отчаивайтесь. Проставки вполне можно найти на любом автомобильном рынке. Только не ожидайте от них каких-либо невероятных чудес. Клиренс увеличится всего на 12-15 мм. Хотя этого недостаточно при пересечении глубоких ям и ухабин, зато вполне может выручить во время встречи с «лежачим полицейским».
Более того, вмешательство в устройство автомобиля посредством проставок считается вполне безопасным, а потому вы можете не страшиться того, что оно негативно скажется на поведении автомобиля.
Развивая тему безопасности, следует вспомнить о целесообразности покупки пластиковых проставок как более надежных.
Видоизмененные амортизаторы
Как правило, заводской амортизатор не оказывает никакого воздействия на величину клиренса. Но если вы работаете с уже изношенном узлом, то во время движения он может подвергнуться раскачиванию в прямом направлении, благодаря чему сильно увеличивается возможность получения повреждений не только бампера, но и расположенных под днищем автомобиля компонентов и деталей Лады.
Для того чтобы качественно увеличить клиренс на «Приору» (данное правило актуально и для любого другого автомобиля), следует пользоваться только оригинальными амортизаторами, которые будут отличаться от заводских по ряду характеристик. Так, например, на них будет увеличена длина штока, длина пружины и сильно повысится качество жесткости пружины. Последнее достигается благодаря настройке амортизаторов — утолщению витков.
Следует заметить, что увеличение параметров амортизатора является достаточно дорогим способом изменения клиренса. Именно поэтому им пользуются редко. Однако возможности для работы с амортизаторами весьма велики, поскольку можно использовать не только узлы Лады, но еще и компоненты иных машин. Кроме того, существуют специальные предложения от фирм-производителей узлов, которые позволяют добиться увеличения клиренса.
Именно поэтому им пользуются редко. Однако возможности для работы с амортизаторами весьма велики, поскольку можно использовать не только узлы Лады, но еще и компоненты иных машин. Кроме того, существуют специальные предложения от фирм-производителей узлов, которые позволяют добиться увеличения клиренса.
То, насколько велик дорожный просвет автомобиля «Лада Приора», будет зависеть от того, какая на нем установлена пружина. Поскольку кузов будет крепиться именно на ней, то от величины жесткости пружины и расстояния от ее нижней точки до верхней будет зависеть не только дорожный просвет, но и качество работы подвески в целом.
Вариантов того, какие пружины крепить на интересующий нас автомобиль, существует не слишком много. Всего есть 2 класса: А и Б, из которых более ранний вариант считается самым жестким. Еще существуют и некоторые разновидности пружин, устанавливающихся на машину во время заводской сборки. Качественно изменив их, мы также можем увеличить дорожный просвет.
Но не забывайте, что стремление к получению чрезмерной жесткости пружин может привести к непредвиденным последствиям. Так, например, вы можете добиться подпрыгивания автомобиля во время встречи с кочками и «лежачими полицейскими». Жесткость пружины очень полезна тогда, когда машина имеет большой вес или сильно перегружена. Однако налегке будет ухудшена работа подвески, и она не сможет работать плавно.
Так, например, вы можете добиться подпрыгивания автомобиля во время встречи с кочками и «лежачими полицейскими». Жесткость пружины очень полезна тогда, когда машина имеет большой вес или сильно перегружена. Однако налегке будет ухудшена работа подвески, и она не сможет работать плавно.
Загрузка …Если вы все-таки решили увеличить жесткость, то можно посоветовать вам использование межвитковых проставок. Они крепятся прямо на пружину, не позволяя ей сжиматься полностью. Благодаря этому увеличится дорожный просвет, который позволит избежать повреждений во время езды по плохим дорогам.
Lada Priora — обзор, цены, видео, технические характеристики Лада Приора
Lada Priora – это семейство легковых автомобилей, выпускаемых компанией «АвтоВАЗ». Модель имеет заводской индекс ВАЗ-2170. Производство машин началось в 2007 году. В марте 2007 года производитель выпустил более тысячи единиц Lada Priora в кузове седан. В апреле автомобиль поступил в открытую продажу. Практически через год началось производство авто в кузове хэтчбек. А в октябре 2008 года на моторшоу в Краснодаре дебютировала модификация с кузовом универсал. Выпуск этой модели начался в мае 2009 года. Кроме обозначенных версий машин АвтоВАЗ также производит Lada Priora в кузове купе, но объемы выпуска этой модели достаточно малы. Еще одна мелкосерийная модель – Lada Priora Premier. Этот автомобиль – удлиненная на 17,5 сантиметров версия седана. Он производится на тольяттинском заводе ЗАО «Супер-Авто» с 2008 года. Модель комплектуется 1,8-литровым мотором мощностью в 100 лошадиных сил. На основе купе планировалось создать машину с кузовом кабриолет. В начале 2009 года семейство Lada Priora полностью вытеснило с производства серию Lada 110. На освобожденных конвейерах было запущено производство универсалов.
Модель имеет заводской индекс ВАЗ-2170. Производство машин началось в 2007 году. В марте 2007 года производитель выпустил более тысячи единиц Lada Priora в кузове седан. В апреле автомобиль поступил в открытую продажу. Практически через год началось производство авто в кузове хэтчбек. А в октябре 2008 года на моторшоу в Краснодаре дебютировала модификация с кузовом универсал. Выпуск этой модели начался в мае 2009 года. Кроме обозначенных версий машин АвтоВАЗ также производит Lada Priora в кузове купе, но объемы выпуска этой модели достаточно малы. Еще одна мелкосерийная модель – Lada Priora Premier. Этот автомобиль – удлиненная на 17,5 сантиметров версия седана. Он производится на тольяттинском заводе ЗАО «Супер-Авто» с 2008 года. Модель комплектуется 1,8-литровым мотором мощностью в 100 лошадиных сил. На основе купе планировалось создать машину с кузовом кабриолет. В начале 2009 года семейство Lada Priora полностью вытеснило с производства серию Lada 110. На освобожденных конвейерах было запущено производство универсалов. Начать выпуск следующего поколения Lada Priora производитель планирует в 2016 году.
Начать выпуск следующего поколения Lada Priora производитель планирует в 2016 году.
Автомобиль Lada Priora Coupe, имеющий заводской индекс ВАЗ-2172, представляет собой мелкосерийную модель АвтоВАЗа выпускающуюся в трехдверном кузове хэтчбек. Машина сконструирована на платформе Lada Priora. Авто должно заменить модель ВАЗ-21123. Производство Priora в кузове трехдверный хэтчбек началось в 2010 году. Оригинальная Priora в кузове седан производится с 2007 года. Первый пятидверный хэтчбек сошел с конвейера лишь через год. Для нового автомобиля конструкторы разработали более 150 оригинальных элементов, в том числе детали каркаса, передние двери, стекла, диски и так далее. Машина получила складные спинки передних сидений, а сами кресла были усилены. Для выпуска автомобиля было задействовано опытно-промышленное производство АвтоВАЗа. Ранее здесь производился предшественник Priora Coupe, от которого машина отличается более удобным салоном, более мощным двигателем и расширенной комплектацией. Перед запуском в серийное производство Lada Priora Сoupe была подвергнута испытаниями. Сообщается, что показатели краш-тестов полностью удовлетворяют нормативам, принятым в России. На основе данной модели производитель планировал создать кабриолет.
Перед запуском в серийное производство Lada Priora Сoupe была подвергнута испытаниями. Сообщается, что показатели краш-тестов полностью удовлетворяют нормативам, принятым в России. На основе данной модели производитель планировал создать кабриолет.
Увеличить дорожный просвет на 30-50 мм с подвеской CROSS20.
Одной из важных характеристик подвески автомобиля является клиренс. Клиренс автомобиля — это расстояние от наиболее низких частей автомобиля, таких как редукторы, элементы выхлопной системы или защита агрегатов, до поверхности дороги. Величина клиренса или, как его часто называют, дорожного просвета во многом определяет универсальность автомобиля. По сути, увеличенный клиренс позволяет вам без опасения за бамперы и днище автомобиля парковаться в любом месте, уверенно проезжать «лежачих полицейских», выезжать за город на проселочные дороги и нормально двигаться по снегу и колеям в зимнее время года. Немаловажно, что высокий клиренс позволяет расширить обзор, что повышает безопасность движения как в плотном потоке машин, так и на загородной трассе.
Если вы решили, что ваш автомобиль должен иметь увеличенный клиренс, то можете выбрать между полноценными рамными внедорожниками, кроссоверами или модификациями обычных автомобилей с увеличенным клиренсом (например, Renault Sandero Stepway). У каждого из этих вариантов есть свои плюсы и минусы, а большая разница в цене между внедорожниками, кроссоверами и модификациями с увеличенным дорожным просветом делает последние достаточно выгодным приобретением.
Что подтолкнуло нас к созданию внедорожной подвески для автомобилей ВАЗ?
Появление на авторынке кроссоверов с моноприводом (псевдокроссоверов) вызвано необходимостью адаптировать популярные марки автомобилей к более тяжёлым дорожным условиям в России. Псевдокроссовер — автомобиль с увеличенным дорожным просветом и диаметром колес, а также усиленной подвеской — более приспособлен к нашим дорогам и зимним дорожным условиям. Создание кроссовера с существенным улучшением ходовых свойств на базе «Калины» и стало целью создания подвески CROSS20.
Если вы решили в корне преобразить ваш автомобиль, значительно улучшив его управляемость, устойчивость, комфортность, надёжность и проходимость, то компания SS20 предлагает вам комплект подвески CROSS20, в котором изменения коснулись следующих элементов:
- передних амортизаторов,
- задних амортизаторов,
- приводов,
- нижнего рычага,
- переднего стабилизатора,
- рулевого механизма,
- сайлентблоков,
- появился задний стабилизатор.
В результате комплекса этих изменений, при установке подвески CROSS20 вы получаете следующие преимущества:
- Повышенная геометрическая проходимость и высокая посадка, присущая кроссоверам, обеспечены за счет увеличения клиренса до 50 мм.
- Расширенная на 30мм колея дает большую устойчивость автомобиля.
- Увеличивается плавность хода за счет изменения настроек амортизаторов и жесткости сайлентблоков.
- Улучшаются ходовые свойства автомобиля.
- Оптимальное соотношение жесткостей переднего и заднего стабилизаторов поперечной устойчивости уменьшает крены кузова при поворотах и маневрировании; при этом обеспечивается надежное сцепление колес с дорогой.

Увеличение клиренса на 30 мм обеспечивается конструкцией передних и задних амортизаторов с удлиненным корпусом и специальными настройками клапанной системы. Дополнительное увеличение клиренса на 20 мм достигается при замене штатной шины размерностью 175/65 R14 и диска R14 на шину 185/65 R15 с диском R15.
Благодаря измененной конструкции передних рычагов и кронштейнов крепления происходит расширение колеи на 30 мм.
Передний стабилизатор с креплением на стойку более эффективен, он увеличивает устойчивость автомобиля на дороге и снижает крены в поворотах. Для дополнительного противодействия кренам в состав подвески CROSS20 входит задний стабилизатор поперечной устойчивости, отсутствующий в заводской комплектации автомобиля.
Модифицированная конструкция сайлентблоков в передней и задней подвеске с измененной жесткостью и геометрическими размерами несколько улучшает кинематику подвесок и также направлена на увеличение комфорта во время поездки.
На сегодняшний момент подвеска CROSS20, увеличивающая дорожный просвет, изготавливается на следующие автомобили:
- ВАЗ 2108,
- ВАЗ 2110,
- ВАЗ 2170-72 (Приора),
- ВАЗ 1117-19 (Калина),
- ВАЗ 2190 (Гранта).

Гарантия на подвеску CROSS20 составляет 1 год без ограничения пробега. Гарантийное обслуживание осуществляется независимо от того, устанавливалась система увеличения клиренса самостоятельно или в сервисном центре.
Клиренс Лады Приоры (отзывы реальных владельцев)
Здесь содержится информация о дорожном просвете (клиренсе) Лады Приоры. Опубликована официальная информация (по паспорту) и отзывы реальных владельцев данного автомобиля.
Вы также можете высказать свое мнение, написав его в форме комментирования, расположенной в нижней части страницы.
| Модификация | Клиренс |
| Универсал | 165 |
| Хэчбек | 165 |
| Купе | 165 |
Отзывы владельцев Лады Приоры
- Полгода назад по необходимости купил себе Ладу Приору.
 В целом машина меня устраивает. Днищем не чиркает. Ездил пока только на дачу- клиренс нормальный.
В целом машина меня устраивает. Днищем не чиркает. Ездил пока только на дачу- клиренс нормальный.
- Готов рассказать – я с другом у него Форд третий я на Приоре по проселке гонялись. Так вот ямы, ухабы и прочие неровности дороги благодаря высокому зазору хватает на ура. А мой друг брюхом греб.
- Высота зазора не плохая, по Питеру великолепно не задевает бордюры, лежачих ментов не цепляет. Однако стоит отметить, это не внедорожник для проселке не подойдет.
- Каждые выходные аккуратно по сельской дороге катаюсь, просвет в норме подойдет для безобразных дорог.
- Я дачник машина забита под завязку. Солидный клиренс нечего сказать! Еще ни разу брюхом кочки не зацепил.
- У нас в деревне дорога ужасная – колея, глина, ямы, ухабы. Вообще отвратительная. Катаюсь на Приоре днищем ни разу ни задел. Доволен, клиренс для этих дорог не плох.
- У меня раньше была иномарка, ездил через полицейских как на катке, а на Приоре такого нет – дорожный просвет суперский! Для наших дорог делали.

- Автомобиль катаю не только по населенному пункту, но и частенько выбираюсь за город и даже межгород катаюсь. Высота дорожного просвета 17 см велик особенно для такого авто.
- Представляете, мы с друганами решили тачку обкатать трое приятелей сели на заднее сидение и поехали. Вы не поверите, сложилось такое впечатление, что машина на пузо легла. Все бугорки и ямки чувствовались очень сильно. Просвет в целом не плох цепанули пару раз. Но все, же по проселке ехать на скорости будет очень рисково.
- Цепляет зараза по сильному бездорожью, на буграх брюхом трет, а так к бордюрам нормально можно парконутся, проходят почти все, кроме большущих паребриков. Лежачих проходит хорошо.
- Однажды мы отправились в деревню по проселке и создалось впечатление, что после нашей поездки дорога станет ровнее все бугры дном цепляли.
- Нормальный клиренс. Бывает во много раз хуже. У меня был европеец, вот там ужас – как пылесос собирал все бугры, очень низкая.

- Действительно нечего сказать, просвет низкий, до этого момента и на предыдущих тачках проходил везде, сейчас страшно лезть, куда попало она у меня еще новая, только полгода пользую. Но, безусловно, это не кроссовер и если не заморачиваться катаясь по бездорожью, то для города хватит клиренса.
Предварительная информация для популяционного фармакокинетического и фармакокинетического / фармакодинамического анализа: обзор и руководство с акцентом на подпрограмму NONMEM PRIOR
Определение эталонной модели
Какой бы метод ни использовался для интеграции предыдущих знаний в новую модель, первый шаг состоит в определении наиболее актуальная эталонная модель с эталонными параметрами, которые будут реализованы как предварительные («гиперпараметры»). Если доступно более одной предыдущей модели, эталонная модель может быть выбрана среди них с использованием различных критериев, представленных в разделе «Выбор одной модели».Помимо выбора модели, можно объединить несколько моделей либо в «комбинированную модель», либо с помощью «метаанализа со случайными эффектами» (раздел «Объединение нескольких моделей»). Если доступна только одна предыдущая модель или когда выбрана или построена одна эталонная модель, ее актуальность в качестве эталонной модели можно оценить с помощью методов, представленных в разделе «Устойчивость эталонной модели».
Если доступна только одна предыдущая модель или когда выбрана или построена одна эталонная модель, ее актуальность в качестве эталонной модели можно оценить с помощью методов, представленных в разделе «Устойчивость эталонной модели».
Выбор одной модели
Эмпирический выбор
Если доступно несколько предыдущих моделей, эталонная модель может быть выбрана среди них на основе (i) сходства населения ( e.грамм. аналогичных демографических характеристик [6], тот же географический регион [18]), (ii) количество соответствующих оцененных структурных параметров [12], (iii) уверенность в оценке (оценках) интересующего (их) параметра (ов), согласно дизайну исследования. Например, Kshirsagar et al. хотел оценить константу поглощения с помощью Prior [35]. Их эталонная модель была построена на самой высокой доле данных (17%) в период раннего поглощения (до 2 часов) по сравнению с другими опубликованными моделями.
Критерии качества байесовской оценки на новых данных
Knosgaard et al . сравнил литературные модели относительно их производительности в качестве байесовского аттрактора для оценки индивидуальных параметров ПК по новым данным, чтобы выбрать наиболее адаптированную предыдущую модель для использования в подпрограмме PRIOR [9]. Во-первых, байесовская оценка индивидуальных параметров ПК для каждой модели была проведена на новых данных (MAXEVAL = 0 на этапе оценки позволяет оценить индивидуальный η в зависимости от начальных оценок). Затем модели были ранжированы по OFV или информационному критерию Акаике (AIC, который применяет штраф к моделям с большим количеством параметров).Для каждой модели плотности распределения отдельных η i сравнивались с теоретическим η-распределением \ (N \) (0, ω 2 ). Была выдвинута гипотеза, что модель адекватно описывает новый набор данных, если распределения визуально перекрываются и η-усадка низкая, как показано на рис. 1.
сравнил литературные модели относительно их производительности в качестве байесовского аттрактора для оценки индивидуальных параметров ПК по новым данным, чтобы выбрать наиболее адаптированную предыдущую модель для использования в подпрограмме PRIOR [9]. Во-первых, байесовская оценка индивидуальных параметров ПК для каждой модели была проведена на новых данных (MAXEVAL = 0 на этапе оценки позволяет оценить индивидуальный η в зависимости от начальных оценок). Затем модели были ранжированы по OFV или информационному критерию Акаике (AIC, который применяет штраф к моделям с большим количеством параметров).Для каждой модели плотности распределения отдельных η i сравнивались с теоретическим η-распределением \ (N \) (0, ω 2 ). Была выдвинута гипотеза, что модель адекватно описывает новый набор данных, если распределения визуально перекрываются и η-усадка низкая, как показано на рис. 1.
График отдельных η зазоров (черная линия) поверх теоретическое η-распределение N (0, ω 2 ) (пунктирная линия). Модель, приводящая к верхнему графику, должна быть предпочтительнее модели, приводящей к нижнему графику.ETACL: η зазоров. Адаптировано из [43]
Модель, приводящая к верхнему графику, должна быть предпочтительнее модели, приводящей к нижнему графику.ETACL: η зазоров. Адаптировано из [43]
Прогностическая эффективность каждой модели может быть оценена с помощью нескольких симуляций, которые затем сравниваются с новыми данными:
Визуальные прогностические проверки (VPC) могут быть построены с новыми данными (внешний VPC).
Нормализованные ошибки распределения прогнозов (NPDE) можно использовать для сравнения смоделированных концентраций с данными наблюдений в новом наборе данных [37]. Затем модели можно сравнивать и ранжировать в соответствии с p-значениями тестов, определяющих, следуют ли NPDE нормальному распределению (t-критерий ранжирования знаков Вилкоксона, критерий Фишера для дисперсии, критерий Шапиро-Уилкса).Лучшая прогностическая модель — это та, которая дает наименьшее количество тестов, в которых NPDE отклоняются от нормального распределения.
При систематическом сравнении литературных моделей, проведенном Knosgaard et al. , Прогностическая эффективность моделей была более четко дифференцирована по NPDE, чем по VPC.
, Прогностическая эффективность моделей была более четко дифференцирована по NPDE, чем по VPC.
Объединение нескольких моделей
Мета-анализ со случайным эффектом
Milosheska et al . выполнил метаанализ со случайными эффектами для определения значений эталонных параметров и их неопределенности [23].В этом методе значения параметров из структурно идентичных моделей усредняются, взвешиваясь по их неопределенности. В отличие от метаанализа с фиксированным эффектом, метаанализ со случайными эффектами предполагает, что включенные исследования не принадлежат к одной и той же популяции, и выдвигает гипотезу о том, что существует распределение истинной величины эффекта от «вселенной» популяций ( Рис. 2 ). Метаанализ со случайными эффектами может быть легко реализован в программе R [38].
Фиг.2Иллюстрация параметров модели случайных эффектов из [38]. \ (\ widehat {\ theta} \) k = μ + ϵk + ζk (1), \ (\ widehat {\ theta} k \): типичное значение в исследовании k, μ: типичное значение во «вселенной» совокупность, ϵk: отклонение от типичного значения из-за ошибок выборки в исследовании k, ζk: отклонение от типичного значения из-за всеобъемлющего распределения истинных величин эффекта со средним, μ, ζk ~ N (μ, τ 2 )
Комбинированная модель
При необходимости эталонная модель может объединять модели из двух (или более) исследований, имеющих разную направленность и предоставляющих дополнительную информацию. Knosgaard et al. проанализировали как исходное лекарство, так и метаболит: они объединили модель исходного лекарственного средства и модель метаболита, которая показала наилучшие результаты на этапе систематического сравнения моделей для каждой молекулы [9]. Brill et al., . построил модель для количественной оценки эффекта взаимодействия антиретровирусных препаратов на лечение туберкулеза у пациентов с ВИЧ и туберкулезом [7]. Параметры PK противотуберкулезного препарата были основаны на данных двух исследований фазы IIb с участием субъектов, не принимавших антиретровирусные препараты.Параметры эффекта лекарственного взаимодействия основывались на данных двух исследований лекарственного взаимодействия у субъектов без туберкулеза.
Knosgaard et al. проанализировали как исходное лекарство, так и метаболит: они объединили модель исходного лекарственного средства и модель метаболита, которая показала наилучшие результаты на этапе систематического сравнения моделей для каждой молекулы [9]. Brill et al., . построил модель для количественной оценки эффекта взаимодействия антиретровирусных препаратов на лечение туберкулеза у пациентов с ВИЧ и туберкулезом [7]. Параметры PK противотуберкулезного препарата были основаны на данных двух исследований фазы IIb с участием субъектов, не принимавших антиретровирусные препараты.Параметры эффекта лекарственного взаимодействия основывались на данных двух исследований лекарственного взаимодействия у субъектов без туберкулеза.
Надежность эталонной модели
Критерии качества, перечисленные в разд. 3.1.1 можно оценить на выбранной, построенной или единственной эталонной модели. Внешние VPC также использовались Perez-Ruixo et al. чтобы подтвердить способность модели ПК с аллометрическим масштабированием, разработанной для взрослых, описывать педиатрические данные [26]. VPC с поправкой на внешнее предсказание (pcVPC) использовали Deng et al . и Магнуссон и др. . , чтобы убедиться, что эталонная модель в целом соответствует новым данным [29, 30].
VPC с поправкой на внешнее предсказание (pcVPC) использовали Deng et al . и Магнуссон и др. . , чтобы убедиться, что эталонная модель в целом соответствует новым данным [29, 30].
Если предыдущие данные доступны, можно оценить способность эталонной модели оценивать с предварительными некоторыми параметрами на подмножестве данных. Маршалл и др. . использовал подпрограмму PRIOR для построения полумеханистической модели с разреженными данными [15]. Эталонная модель включала модель нейтрофилов и комбинированную модель PK и рецептора (рецептор CD11b). Разрозненные данные содержали наблюдения нейтрофилов и PK, но не содержали информации о связывании CD11b (ни измерения свободного, ни общего CD11b), в то время как модель не могла быть упрощена по механистическим причинам.Поскольку предыдущие данные были доступны, можно было оценить силу предыдущих оценок параметров связывания CD11b: модель с предшествующим (предыдущая модель как предшествующая) была построена на предыдущих данных без наблюдений, которые позволили оценить данные связывания CD11b. Устойчивость оценивалась путем оценки степени сходства между оценками этой модели и эталонной модели.
Устойчивость оценивалась путем оценки степени сходства между оценками этой модели и эталонной модели.
Таким образом, в идеале можно выбрать модель, которая лучше всего отвечает поставленной цели ( e.грамм. характеристика ка). Если некоторые модели эквивалентны с точки зрения проблематики, можно либо использовать модель, которая лучше всего описывает новые данные с использованием байесовских критериев качества оценки, либо построить новую модель с метаанализом. В некоторых случаях описываемый процесс требует комбинации двух или более дополнительных моделей, которые имеют разную направленность.
Следует отметить, что эталонные параметры могут быть адаптированы к целевой группе населения. Например, для анализа фармакокинетики у беременных Lohy Das et al.использовали эталонную модель, построенную как на беременных, так и на небеременных женщинах, которые включали беременность в качестве значимой ковариаты для межкапартаментного клиренса: эталонная оценка межкапартментного клиренса была рассчитана с учетом эффекта беременности [19].
Независимо от выбранной эталонной модели ее надежность следует оценивать с помощью байесовской оценки новых данных и / или внешнего VPC.
Код для предоставления предварительной информации о подпрограмме $ PRIOR
Подпрограмма NWPRI или TNPRI?
Можно вызвать два типа подпрограмм PRIOR: $ PRIOR NWPRI или $ PRIOR TNPRI, в зависимости от предположения о распределении предшествующих параметров.Действительно, априорные параметры можно рассматривать как нормально распределенные или обратно-распределенные Вишарта [3]. В NWPRI (наиболее распространенном) фиксированные параметры THETA предполагаются нормально распределенными, а случайные параметры OMEGA 2 (межиндивидуальная и / или межсезонная изменчивость) предполагаются обратным распределением Вишарта. В TNPRI оба считаются нормально распределенными.
Методическая статья Gisleskog et al. подчеркивает теоретическое преимущество использования TNPRI по сравнению с NWPRI: в отличие от нормально-обратного распределения Уишарта (NWPRI), нормально-нормальное распределение (TNPRI) может выражать корреляции между отдельной информацией об отдельных значениях THETA и OMEGA 2 [ 3]. Однако в моделировании и тестах, представленных в этой статье, оба метода показали одинаковый процент отклонения оценок параметров и стандартных ошибок от их истинных значений.
Однако в моделировании и тестах, представленных в этой статье, оба метода показали одинаковый процент отклонения оценок параметров и стандартных ошибок от их истинных значений.
В нашем обзоре только две из 32 статей, анализирующих разреженные данные, использовали TNPRI [15, 29]: в обеих статьях предыдущий анализ был проведен одной и той же командой. Восемнадцать статей [4,5,6,7,8,9,10,11,12,13,14, 23, 25, 27, 30, 32,33,34] использовали NWPRI; в остальных 12 статьях метод не был указан [16,17,18,19,20,21,22, 24, 26, 28, 31, 35], из которых шесть использовались ранее только на THETA [19, 20, 22 , 24, 28, 35], поэтому распределение, приписываемое OMEGA, не имело никакого влияния.
На практике реализация NWPRI в NONMEM намного проще, чем реализация TNPRI. В текущей версии NONMEM 7.4 TNPRI требуется выходной файл из эталонной модели (файл msf), который недоступен при использовании априорных значений из литературы.
Предыдущие значения параметров
Предыдущие значения THETA, OMEGA 2 и SIGMA 2 должны быть записаны и зафиксированы в потоке управления в записях $ THETAP, $ OMEGAP и $ SIGMAP соответственно. В случае наличия ковариаций между случайными компонентами n , матрицы OMEGA 2 и SIGMA 2 должны быть указаны в записях $ OMEGAP BLOCK ( n ) и $ SIGMAP BLOCK (n).
В случае наличия ковариаций между случайными компонентами n , матрицы OMEGA 2 и SIGMA 2 должны быть указаны в записях $ OMEGAP BLOCK ( n ) и $ SIGMAP BLOCK (n).
Хотя изменчивость между случаями отличается от изменчивости между индивидуумами, это также случайный эффект, кодируемый с помощью OMEGA. Таким образом, предыдущая межфирменная изменчивость кодируется так же, как и предыдущая межличностная изменчивость.
Обычно реализации априорных значений в SIGMA 2 можно избежать, поскольку данные содержат надежную информацию для оценки остаточной ошибки.В большинстве статей остаточная ошибка оценивалась независимо от исходной модели. Только в двух статьях использовались информативные априорные точки на SIGMA 2 [7, 29], но без объяснения причин.
В четырех из 33 рассмотренных статей использовалось логарифмическое преобразование для параметров фиксированного эффекта модели ПК (THETA) [4, 8, 11, 12]. Следует отметить, что три модели «popPBPK» (см. Раздел 3.8) использовали этот подход, чтобы избежать отрицательных значений выборки для клиренса и сродства к ткани [4, 8, 11]. Лог-преобразование обеспечивает стабильность в процессе оценки [12].2, где RSE = SE (THETA) / THETA.
Раздел 3.8) использовали этот подход, чтобы избежать отрицательных значений выборки для клиренса и сродства к ткани [4, 8, 11]. Лог-преобразование обеспечивает стабильность в процессе оценки [12].2, где RSE = SE (THETA) / THETA.
Вес априорных
Вес каждой априорной модели определяется распределением априорного параметра. Для предполагаемого нормально распределенного априорного параметра вес обратно пропорционален его дисперсии: чем точнее априорный параметр, тем более информативной является модель. Когда предполагается, что априорный параметр имеет обратное распределение Уишарта, его вес пропорционален степени свободы.
Нормально распределенные параметры (предполагаемые для THETA в NWPRI и для THETA и OMEGA 2 для TNPRI) взвешиваются по их матрице дисперсии-ковариации в записи $ THETAPV BLOCK.Когда нужно взвешивать только один нормально распределенный параметр, следует использовать $ THETAPV вместо $ THETAPV BLOCK. Матрица дисперсии-ковариации может быть вычислена из SE предыдущей модели или из непараметрического бутстрапа этой модели, если SE не предоставлены [10]. Большая дисперсия устанавливает неинформативные априорные значения (например, 10 6 [12]). Для информативных априоров предпочтительнее использовать полную ковариационную матрицу. Однако эта информация не всегда доступна, и когда она доступна, это может привести к проблемам с минимизацией.В этих случаях для недиагональных элементов следует установить либо 0 [10], либо очень маленькое значение (например, 10 −7 ). Обнуление недиагональных элементов означает отсутствие корреляции между фиксированными и случайными эффектами, что теоретически может привести к потенциальной систематической ошибке в оценках модели, но на сегодняшний день по этой теме ничего не опубликовано.
Большая дисперсия устанавливает неинформативные априорные значения (например, 10 6 [12]). Для информативных априоров предпочтительнее использовать полную ковариационную матрицу. Однако эта информация не всегда доступна, и когда она доступна, это может привести к проблемам с минимизацией.В этих случаях для недиагональных элементов следует установить либо 0 [10], либо очень маленькое значение (например, 10 −7 ). Обнуление недиагональных элементов означает отсутствие корреляции между фиксированными и случайными эффектами, что теоретически может привести к потенциальной систематической ошибке в оценках модели, но на сегодняшний день по этой теме ничего не опубликовано.
Распределенные параметры обратного Вишарта (предполагаемые для OMEGA 2 и SIGMA 2 в NWPRI) взвешиваются по степени свободы в записях $ OMEGAPD и $ SIGMAPD.Их значения, как и для нормально распределенных параметров, зависят от предполагаемой априорной информативности.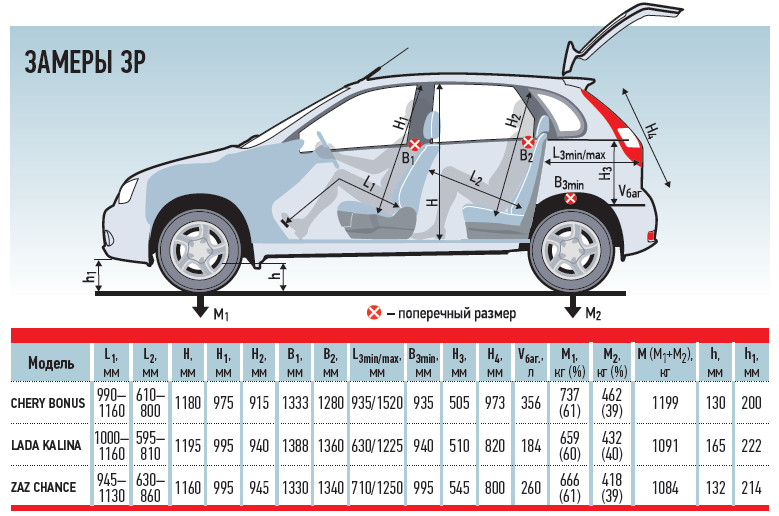 Они могут варьироваться от m + 1, где m — размер матрицы OMEGA или SIGMA, для неинформативных априорных значений, до количества субъектов (для OMEGA) или количества наблюдений (для SIGMA) в предыдущем исследовании для очень информативных априорных значений. Обычно степень свободы для информативных OMEGA рассчитывается по формуле df = 2 * [OMEGA 2 / (SE of OMEGA 2 )] 2 + 1 [1, 6, 11, 23, 39].Та же самая формула может быть применена для информативных СИГМА. Степени свободы относятся ко всему блоку OMEGA, включая недиагональные элементы. Тем не менее, это общий или неопределенный параметр силы, который придает большую силу всем элементам блока OMEGA. Если в предыдущем блоке OMEGA задана высокая степень свободы, и в этом блоке 0 вне диагоналей, тогда как данные указывают на сильную недиагональ, анализ может быть скомпрометирован. Если предыдущие данные доступны, степени свободы обратного распределения Уишарта для OMEGA могут быть оценены с использованием максимального правдоподобия на основе функции плотности вероятности обратного распределения Уишарта, например, с пакетами R mle и diwish [7], или как автоматически оценивается при повторной выборке важности выборки (SIR) [40].
Они могут варьироваться от m + 1, где m — размер матрицы OMEGA или SIGMA, для неинформативных априорных значений, до количества субъектов (для OMEGA) или количества наблюдений (для SIGMA) в предыдущем исследовании для очень информативных априорных значений. Обычно степень свободы для информативных OMEGA рассчитывается по формуле df = 2 * [OMEGA 2 / (SE of OMEGA 2 )] 2 + 1 [1, 6, 11, 23, 39].Та же самая формула может быть применена для информативных СИГМА. Степени свободы относятся ко всему блоку OMEGA, включая недиагональные элементы. Тем не менее, это общий или неопределенный параметр силы, который придает большую силу всем элементам блока OMEGA. Если в предыдущем блоке OMEGA задана высокая степень свободы, и в этом блоке 0 вне диагоналей, тогда как данные указывают на сильную недиагональ, анализ может быть скомпрометирован. Если предыдущие данные доступны, степени свободы обратного распределения Уишарта для OMEGA могут быть оценены с использованием максимального правдоподобия на основе функции плотности вероятности обратного распределения Уишарта, например, с пакетами R mle и diwish [7], или как автоматически оценивается при повторной выборке важности выборки (SIR) [40]. Целью SIR является аппроксимация истинной неопределенности параметров [41]. Векторы параметров выбираются из ковариационной матрицы, и модель запускается на данных с каждым набором параметров с использованием максимальной апостериорной байесовской оценки (MAXEVAL = 0). Когда модель строится с использованием предыдущей подпрограммы, ковариационная матрица берется из предыдущей модели. Затем параметры подвергаются повторной выборке в соответствии с коэффициентом важности, вычисленным на предыдущем шаге. Эта передискретизация повторяется. А затем для каждой OMEGA обратное распределение Вишарта может быть адаптировано к распределению передискретизированного OMEGA: степень свободы обратного распределения Вишарта — это та, которая может быть указана в $ OMEGAPD.
Целью SIR является аппроксимация истинной неопределенности параметров [41]. Векторы параметров выбираются из ковариационной матрицы, и модель запускается на данных с каждым набором параметров с использованием максимальной апостериорной байесовской оценки (MAXEVAL = 0). Когда модель строится с использованием предыдущей подпрограммы, ковариационная матрица берется из предыдущей модели. Затем параметры подвергаются повторной выборке в соответствии с коэффициентом важности, вычисленным на предыдущем шаге. Эта передискретизация повторяется. А затем для каждой OMEGA обратное распределение Вишарта может быть адаптировано к распределению передискретизированного OMEGA: степень свободы обратного распределения Вишарта — это та, которая может быть указана в $ OMEGAPD.
На рисунке 3 показано, как кодировать предыдущий вес в контрольном файле. Неинформативное распределение также можно назвать расплывчатым [12], поскольку до тех пор, пока используется априорное распределение, оно остается хотя бы немного информативным.
Пример кодов управляющего файла NONMEM для реализации подпрограммы PRIOR, NWPRI, информативных и неинформативных априорных точек; как определено Bauer [1] и Gisleskog et al . [3]
Восемь из 32 статей, анализирующих разреженные данные, реализовали информативные априорные значения по всем параметрам [5, 10, 12, 15, 23, 29,30,31], 18 реализовали информативные априорные значения и / или так называемые «Малоинформативны» (когда они связаны с неопределенностью 10% [20] или 50% [24, 28]) только по части параметров [7,8,9, 13, 16,17,18,19,20 , 21,22, 24, 25, 28, 32,33,34,35] и три реализованных неинформативных априорных значения по некоторым параметрам, в то время как имели информативные априорные значения по остальным параметрам [4, 6, 11].Последнее включало исследование с использованием MCMC [6] и исследование, сравнивающее FOCE с MCMC [4]. В трех статьях не уточняется, насколько информативными были априорные решения [14, 26, 27].
Когда только подмножество параметров оценивается с использованием априорной информации, эти параметры должны быть объявлены первыми в NONMEM: первые n параметров, где n — количество параметров, определенных в операторе $ THETAP и / или $ OMEGAP, будут есть приоры, а по следующим параметрам не будет.
Уменьшение предшествующего веса и даже его подавление полезно для получения максимальной информации от новой популяции.Ковариативный поиск должен проводиться только по параметрам, оцененным без предварительной оценки (см. Раздел 3.6). Более того, если модель с полностью информативными априорными значениями имеет гораздо более высокие оценки межиндивидуальной изменчивости по сравнению с предыдущим значением, это может быть связано с силой предыдущих значений для соответствующих фиксированных эффектов вместе с потенциально другой оценкой параметров популяции в новой популяции. . В этом случае представляется интересным уменьшить априорный вес или удалить априор из этих параметров (по возможности, как для THETA, так и для OMEGA) [7].
Подходы к удалению априорных значений
Чтобы определить, можно ли оценить параметр без предварительной оценки, можно использовать отношение RSE оценок параметров PK из модели, построенной до RSE из предыдущей модели: если отношение RSE очень small, можно рассмотреть возможность удаления априорного значения соответствующего параметра [15] (см. подход Маршалла и др., , в разделе 3.5).
Стивенс и др. . удалил априорные значения из каждого параметра по очереди. Для каждой переоценки они наблюдали влияние на OFV, а также на значение и точность других параметров [34].Они протестировали априорные значения по двум параметрам и решили сохранить априорные значения по обоим: вместе с падением OFV оставшийся параметр имел правдоподобные значения и меньшие доверительные интервалы. Например, когда они удалили предварительное значение ЕС50 препарата (концентрация, вызывающая половину максимального эффекта Emax), оценка Emax увеличилась в три раза и стала менее правдоподобной.
Knosgaard et al . также протестировал различные комбинации априорных значений (, например, . Предшествующий на THETA, с или без предварительного на OMEGA), чтобы выбрать тот, который дает самый низкий OFV [9].
Подходы к выбору априорного веса
Чтобы реализовать наилучший вес априорного веса, Магнуссон и др. . сравнил результаты моделей с информативными априорными значениями, взвешенными, с одной стороны, по заданной 10% неопределенности, а с другой стороны, по их меньшим эталонным неопределенностям в терминах VPC (см. Рис. 2 в исходной статье [30]), остаточной необъяснимая изменчивость, параметры изменчивости между индивидуумами и случаями. В этом случае модель с 10% -ной неопределенностью, присвоенной параметрам модели, обеспечивала наиболее адекватное описание данных и уменьшала параметры изменчивости.
В своей педиатрической модели Knebel et al. варьировали информативность априорных данных для взрослых, чтобы минимизировать влияние априорной информации для взрослых, но при этом обеспечить стабильную оценку: дисперсия была установлена на 10 6 для половины THETA (неинформативно), а степень свободы OMEGA была зафиксирована на наименьшее возможное значение (размерность матрицы OMEGA) [12].
Krogh-Madsen et al. также протестировали различные значения степени свободы для OMEGA: в оценках параметров были незначительные изменения.Следовательно, степень свободы в окончательной модели была установлена на минимально возможное значение, считая ее более подходящей для компенсации выбора распределения (например, , , обратное Wishart) [14].
Подводя итог, NWPRI может быть предпочтительнее TNPRI, если нет сильной корреляции между THETA и OMEGA. Приоры на SIGMA 2 следует избегать. Следует использовать различные комбинации и веса априорных значений, чтобы выбрать тот, который работает лучше всего, т. Е. Дает самый низкий OFV, доверительные интервалы, остаточную изменчивость и имеет лучшую прогностическую способность с помощью VPC.
Целевые функции модели, построенной с предыдущей версией
Выходной файл NONMEM отображает два блока информации для OFV для моделей, созданных с предыдущей версией.
Первый такой же, как полученный с моделями без предшествующих:
ОБЩИЕ ТОЧКИ ДАННЫХ, ОБЫЧНО РАСПРЕДЕЛЕННЫЕ (N)
N * LOG (2PI) ПОСТОЯННАЯ ФУНКЦИЯ ОБЪЕКТА
ЦЕЛЕВАЯ ФУНКЦИЯ ЗНАЧЕНИЕ БЕЗ КОНСТАНТЫ: целевая функция для данных, включая предыдущий штраф (обычно сообщаемый) = O S + O P
ЦЕЛЬ ФУНКЦИОНАЛЬНОЕ ЗНАЧЕНИЕ С КОНСТАНТОЙ: сумма двух слагаемых выше
Второй относится к моделям, созданным с предыдущими версиями:
КОНСТАНТА ДО ОБЪЕКТИВНОЙ ФУНКЦИИ: константы, относящиеся к Wisharts OMEGA, SIGMA и нормальному THETA (соответствующий кратный LOG (2PI))
ЦЕЛЕВАЯ ФУНКЦИЯ ЗНАЧЕНИЕ БЕЗ КОНСТАНТЫ: целевая функция для данных, включая предыдущий штраф (такой же, как и в первом блоке) = O S + O P
ЦЕЛЬ ФУНКЦИОНАЛЬНОЕ ЗНАЧЕНИЕ С (ПРЕДВАРИТЕЛЬНАЯ) КОНСТАНТА : сумма двух слагаемых выше
Целевая функция с константой используется только для совместимости с тем, как другое программное обеспечение может сообщать OFV. Предыдущий вклад в целевую функцию (предварительный штраф, O P ) включен в отчетные OFV. OFV для данных (O S ) — это сумма отдельных OFV, указанных в phi-файле выходных данных NONMEM. O S — это OFV, вычисленное с помощью модифицированной модели (модель, в которой начальные оценки были установлены на основе окончательных оценок модели, построенной с априорными значениями), запущенной с MAXEVAL = 0 NOPRIOR = 1 (без предварительной оценки). Затем O P можно рассчитать как разницу между сообщенным OFV без константы и O S .
Предыдущий вклад в целевую функцию (предварительный штраф, O P ) включен в отчетные OFV. OFV для данных (O S ) — это сумма отдельных OFV, указанных в phi-файле выходных данных NONMEM. O S — это OFV, вычисленное с помощью модифицированной модели (модель, в которой начальные оценки были установлены на основе окончательных оценок модели, построенной с априорными значениями), запущенной с MAXEVAL = 0 NOPRIOR = 1 (без предварительной оценки). Затем O P можно рассчитать как разницу между сообщенным OFV без константы и O S .
После того, как априор используется в базовой модели, общий OFV (который включает априорный штраф) может использоваться в тестах отношения правдоподобия (LRT), если в априорную информацию не вносятся изменения. Таким образом, O S не следует использовать в LRT, поскольку предыдущий был задействован в исходной подгонке, поэтому O S не является минимальным OFV (а не положением максимального правдоподобия).
Следовательно, OFV, которое будет использоваться в сравнениях с использованием LRT, — это общий OFV, который сообщается в выходных данных NONMEM (OFV без константы = O S + O P ).
Влияние изменения предыдущего
Milosheska et al. проверили чувствительность параметров модели [23] (i) к предыдущей спецификации, изменив предыдущие значения на -50% и + 50%, и ii) к информативности предшествующей, изменив точность предшествующей спецификации (SE от От — 50% до + 50%) . Влияние изменения предшествующих значений и точности было оценено количественно по результирующему изменению оценки затронутого параметра. Чувствительность модели к весу предшествующего считалась приемлемой, поскольку оценки параметров оставались в пределах ± 15% диапазона, когда SE варьировалось на ± 50%.Если изменение предыдущего значения приводит к идентичным изменениям в оценках параметров, это означает, что новые данные содержат мало информации об этом параметре: предыдущее значение важно в модели, и его следует тщательно определять и доверять.
Lledo-Garcia et al. также варьировала точность всех априорных значений (одновременно сделав менее информативными за счет увеличения их ассоциированной дисперсии в десять раз): изменение было ниже 6% в каждой оценке параметра и, таким образом, было квалифицировано как «очень незначительное» [33].
Denti et al. протестировали различные настройки для предварительного распределения, чтобы показать, что оценки других параметров модели не были существенно затронуты [24].
На сегодняшний день не существует стандартизированного метода для количественной оценки воздействия на модель изменения стоимости и веса априорной модели. Однако рекомендуется количественно оценить как изменение оценки затронутого параметра, так и стабильность других параметров при изменении предыдущего значения и веса.
Различия в параметрах между предыдущей популяцией и новой популяцией
Параметры, реализованные с априорными параметрами, должны быть аналогичными в предыдущей и новой популяциях. В противном случае новые оценки будут ограничены смещенным значением, что приведет к несоответствию модели, построенной с предыдущей. Кроме того, это может повлиять на оценку других параметров. Фармакометристы использовали разные стратегии для проверки гипотезы о сходстве между параметрами в предыдущей и новой популяциях. Некоторые из этих стратегий также можно использовать для характеристики объема информации, предоставленной новым (разреженным и / или небольшим) набором данных, по сравнению с предыдущей информацией.
В противном случае новые оценки будут ограничены смещенным значением, что приведет к несоответствию модели, построенной с предыдущей. Кроме того, это может повлиять на оценку других параметров. Фармакометристы использовали разные стратегии для проверки гипотезы о сходстве между параметрами в предыдущей и новой популяциях. Некоторые из этих стратегий также можно использовать для характеристики объема информации, предоставленной новым (разреженным и / или небольшим) набором данных, по сравнению с предыдущей информацией.
Brill et al . проверил, показало ли одномерное добавление параметра без априорной информации какое-либо существенное улучшение OFV для каждого параметра модели, построенной с использованием полной априорной [7], то есть тестирование каждого параметра, если добавление параметра различия ( , названный DIS), оцененный на основе новых данных без предварительного уведомления, значительно улучшил OFV модели, построенной с помощью предыдущих. Для каждого параметра две модели сравниваются с LRT: одна с параметром, оцененным с помощью априорной оценки (DIS = 0), другая с параметром, оцененным с априорной оценкой, умноженной на (1 + DIS). Это можно сделать с помощью автоматизированного пошагового ковариатного моделирования (SCM) в PsN® [40]: разница в параметрах между предыдущими данными и новыми данными может быть закодирована DIS = 1, отражая разницу между популяциями двух наборов данных [42] ]. Разницу в OFV между двумя моделями следует сравнивать с фактическим уровнем значимости, который можно вычислить с помощью стохастического моделирования и оценки (SSE) в PsN®. Если добавление DIS (оцениваемого только на основе данных) к параметру значительно улучшает OFV, этот параметр отличается для предыдущей и новой популяции.В таком случае более целесообразно либо удалить предшествующее значение из этого параметра, либо принять во внимание DIS. Код для файла конфигурации SCM и команды SSE для текущей ситуации предлагается в онлайн-ресурсе 2. Аналогичным образом, Chotsiri et al. исследовали различия между исследованиями между новым и предыдущим исследованиями, применяя ковариату категориального исследования по всем фармакокинетическим параметрам [18].
Это можно сделать с помощью автоматизированного пошагового ковариатного моделирования (SCM) в PsN® [40]: разница в параметрах между предыдущими данными и новыми данными может быть закодирована DIS = 1, отражая разницу между популяциями двух наборов данных [42] ]. Разницу в OFV между двумя моделями следует сравнивать с фактическим уровнем значимости, который можно вычислить с помощью стохастического моделирования и оценки (SSE) в PsN®. Если добавление DIS (оцениваемого только на основе данных) к параметру значительно улучшает OFV, этот параметр отличается для предыдущей и новой популяции.В таком случае более целесообразно либо удалить предшествующее значение из этого параметра, либо принять во внимание DIS. Код для файла конфигурации SCM и команды SSE для текущей ситуации предлагается в онлайн-ресурсе 2. Аналогичным образом, Chotsiri et al. исследовали различия между исследованиями между новым и предыдущим исследованиями, применяя ковариату категориального исследования по всем фармакокинетическим параметрам [18]. Нормализованное по массе тела воздействие было ниже у детей в возрасте от 2 месяцев до 5 лет из нового исследования, чем у детей старшего возраста из контрольной модели.Поскольку данных, собранных в новом исследовании, было недостаточно для объяснения этого несоответствия, к относительной биодоступности была применена категориальная ковариата «исследования». Физиологические объяснения были только гипотезами.
Нормализованное по массе тела воздействие было ниже у детей в возрасте от 2 месяцев до 5 лет из нового исследования, чем у детей старшего возраста из контрольной модели.Поскольку данных, собранных в новом исследовании, было недостаточно для объяснения этого несоответствия, к относительной биодоступности была применена категориальная ковариата «исследования». Физиологические объяснения были только гипотезами.
Tsamandouras et al. предложил построить оценки параметров, оцененных с помощью априорных значений, поверх распределений, представляющих имеющиеся априорные знания (априорная неопределенность в параметре модели популяции), чтобы визуализировать степень, в которой эти оценки были изменены с априорных значений [11] (рис.4).
Рис. 4Пример графика, предложенного Цамандурасом и др. . [11], данные из [43]. Оценка THETA (CL) в модели, построенной с использованием Priority, составила 12,7 L.h -1 (черная линия). THETA (CL) в эталонной модели составляла 9,89 л / ч -1 и его стандартное отклонение 3,71 л / ч -1 (пунктирные линии)
Marshall et al . предложил подход, основанный на соотношениях оценок параметров и RSE [15]. Они сравнили каждую оценку параметра PK из модели, построенной по предыдущей модели, с оценкой из предыдущей модели и выявили три случая:
предложил подход, основанный на соотношениях оценок параметров и RSE [15]. Они сравнили каждую оценку параметра PK из модели, построенной по предыдущей модели, с оценкой из предыдущей модели и выявили три случая:
Соотношение оценки параметра ~ 1 и соотношения соответствующего RSE ~ 1: разреженные данные не дают информации об этом аспекте модели
Отношение оценки параметра ~ 1 и отношение соответствующего RSE <1: разреженные данные добавляют информацию об этом параметре
Коэффициент оценки параметра ≠ 1 (отношение соответствующего RSE должно быть>> 1): параметр различается между двумя совокупностями; в этом случае параметр не следует оценивать априори.
Этот метод следует применять с осторожностью. Льедо-Гарсия и др. . исследовал отсутствие уменьшения неопределенности по одному параметру по сравнению с предыдущим (отношение RSE близко к единице) [33]. Они зафиксировали параметр, у которого было заметное снижение неопределенности, и оценили LS (продолжительность жизни), параметр, у которого не было уменьшения неопределенности: LS был хорошо оценен без предварительного (низкий RSE). Это показало, что данные действительно содержали информацию о LS. Более того, оценка LS была близка к эталонному значению: эта информация соответствовала предыдущему значению.
Это показало, что данные действительно содержали информацию о LS. Более того, оценка LS была близка к эталонному значению: эта информация соответствовала предыдущему значению.
Для сравнения распределения фармакокинетических параметров у взрослых и детей Perez-Ruixo et al. использовали «параметрический подход начальной загрузки» для набора данных из 12 детей (12 образцов на каждого ребенка) [26]. Они сравнили оценки модели, построенной до теоретического распределения параметров, которое было бы получено, если бы взрослые и дети имели одинаковое распределение параметров. Это теоретическое распределение было получено с помощью стохастического моделирования (с неопределенностью) и оценки.Во-первых, они смоделировали 1000 (новых) педиатрических наборов данных с неопределенностью, используя распределения параметров непараметрического бутстрапа (эталонной) модели взрослых с аллометрическим масштабированием. Затем они оценили параметры модели, построенной с помощью априорной модели для каждого из 1000 смоделированных наборов данных. Распределение этих оцененных параметров составляет теоретическое распределение. Оценки параметров фиксированного эффекта модели, построенной с помощью априорной модели, находились в пределах 95% доверительного интервала теоретического распределения, что подтвердило сходство точечных оценок фармакокинетических параметров между взрослыми и детьми.Напротив, оценки межгрупповой и остаточной вариабельности модели, построенной с использованием предшествующей модели, выходили за пределы 95% -ного доверительного интервала теоретического распределения, что не подтверждало сходства распределения параметров PK между взрослыми и детьми. Авторы предложили этот подход для выявления различий в распределении параметров PK между взрослыми и детьми. Однако этот подход сомнительный, поскольку предшествующий ограничивает оценку педиатрических параметров аналогичной оценке взрослых.Если бы были различия в параметрах PK между детьми и набором данных для взрослых, их было бы трудно найти, поскольку оценки параметров в наборе данных для детей уже ограничены значениями для взрослых.
Распределение этих оцененных параметров составляет теоретическое распределение. Оценки параметров фиксированного эффекта модели, построенной с помощью априорной модели, находились в пределах 95% доверительного интервала теоретического распределения, что подтвердило сходство точечных оценок фармакокинетических параметров между взрослыми и детьми.Напротив, оценки межгрупповой и остаточной вариабельности модели, построенной с использованием предшествующей модели, выходили за пределы 95% -ного доверительного интервала теоретического распределения, что не подтверждало сходства распределения параметров PK между взрослыми и детьми. Авторы предложили этот подход для выявления различий в распределении параметров PK между взрослыми и детьми. Однако этот подход сомнительный, поскольку предшествующий ограничивает оценку педиатрических параметров аналогичной оценке взрослых.Если бы были различия в параметрах PK между детьми и набором данных для взрослых, их было бы трудно найти, поскольку оценки параметров в наборе данных для детей уже ограничены значениями для взрослых. В этой статье то, что авторы интерпретируют как различие в распределении параметров PK (OMEGA), на самом деле может быть различием в параметрах PK, компенсированным завышенным распределением параметров из-за ограниченного смещения в оценках параметров PK.
В этой статье то, что авторы интерпретируют как различие в распределении параметров PK (OMEGA), на самом деле может быть различием в параметрах PK, компенсированным завышенным распределением параметров из-за ограниченного смещения в оценках параметров PK.
В случаях, когда модель на новых данных может быть построена без предварительного ( e.грамм. Приоры используются для стабилизации модели и во избежание триггерной кинетики), ее окончательные значения параметров можно сравнить с таковыми в модели, построенной с помощью предшествующей модели [14, 35].
В случаях, когда доступны предыдущие данные, сходство в распределении параметров PK между популяциями можно оценить путем сравнения результатов моделей, оцененных без предварительного анализа, на объединенных данных, стратифицированных двумя разными подходами [27]. Первая стратификация — это произвольная дихотомия, которая разбивает объединенный набор данных по совокупности (предыдущая и новая совокупности).Вторая стратификация — это случайная дихотомизация, реализованная подпрограммой MIXTURE в NONMEM, которая идентифицирует две субпопуляции с разными параметрами PK.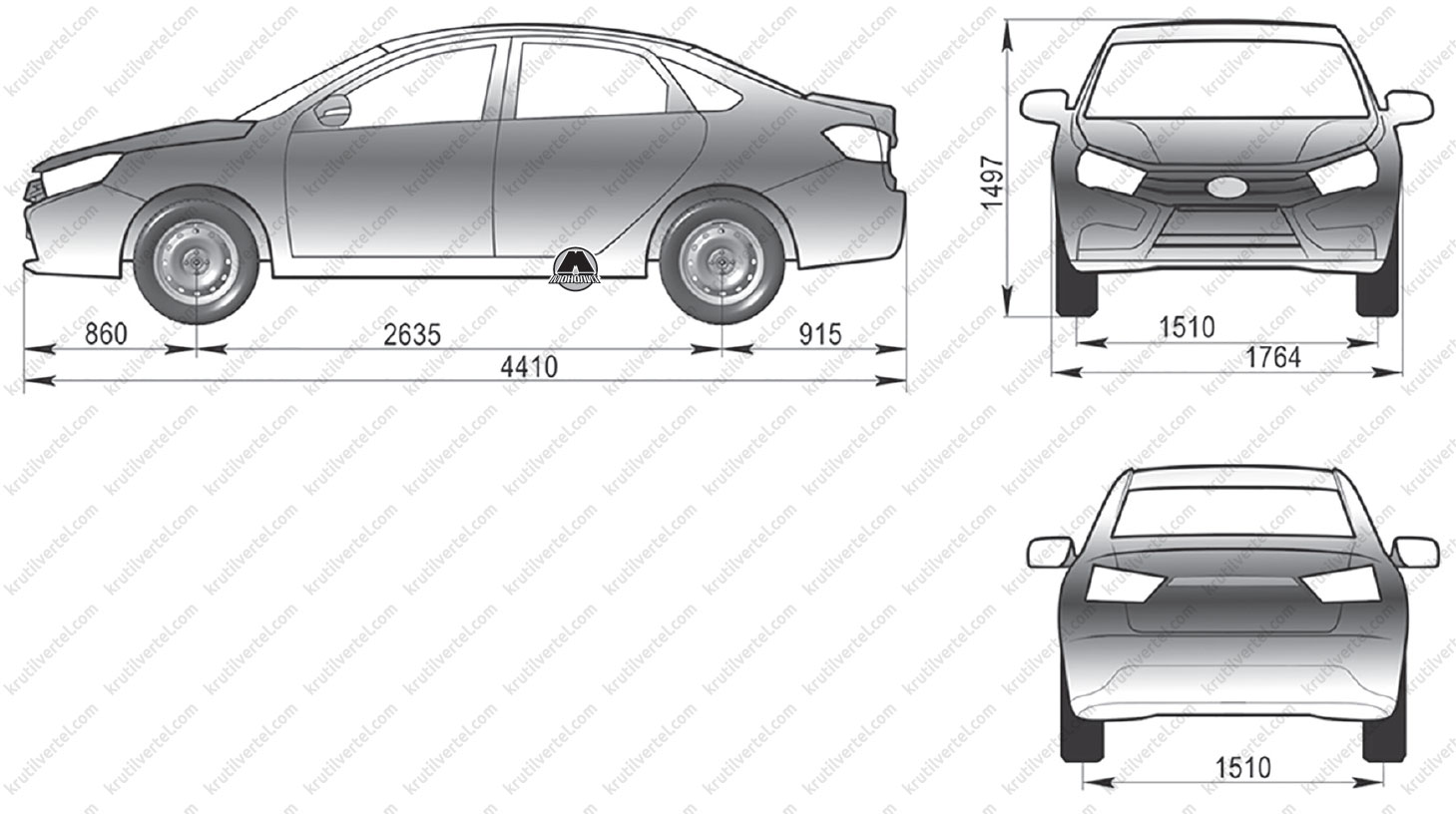 Если предыдущая и новая популяции идентифицируются как субпопуляции при случайной дихотомизации, предыдущая и новая популяции различаются: модель новой популяции не должна интегрировать предыдущую из предыдущей популяции. Если субпопуляции, идентифицированные при случайной дихотомизации, не согласуются с произвольным разбиением, i.е. есть особи как из предыдущей, так и из новой популяции в каждой субпопуляции, предполагается, что предыдущие и новые данные являются частью одной и той же популяции: вариабельность параметров PK может быть описана ковариатами. В этом случае можно оценить на новых данных модель, построенную на основе предыдущей генеральной совокупности.
Если предыдущая и новая популяции идентифицируются как субпопуляции при случайной дихотомизации, предыдущая и новая популяции различаются: модель новой популяции не должна интегрировать предыдущую из предыдущей популяции. Если субпопуляции, идентифицированные при случайной дихотомизации, не согласуются с произвольным разбиением, i.е. есть особи как из предыдущей, так и из новой популяции в каждой субпопуляции, предполагается, что предыдущие и новые данные являются частью одной и той же популяции: вариабельность параметров PK может быть описана ковариатами. В этом случае можно оценить на новых данных модель, построенную на основе предыдущей генеральной совокупности.
В целом выбор метода оценки различий в параметрах между предыдущими и новыми популяциями зависит от ограничений анализа.Если время не является проблемой, тестирование нового исследования как категориальной ковариаты по всем фармакокинетическим параметрам было бы наиболее рекомендуемым подходом, поскольку оно воспроизводимо благодаря автоматизации в PsN. Когда доступны предыдущие данные, сравнение произвольной и случайной стратификаций становится проще.
Когда доступны предыдущие данные, сравнение произвольной и случайной стратификаций становится проще.
Интеграция ковариант
Априорная реализация
Ковариаты эталонной модели могут быть априори включены в модель, построенную с использованием априорной модели, особенно если есть твердое убеждение, что они одинаковы в предыдущей и новой совокупности.Например, помимо аллометрического масштабирования, масштабные коэффициенты для недоношенных новорожденных должны оставаться неизменными: можно предпочесть зафиксировать значения масштабного коэффициента на их предыдущих оценках и оценить стандартизованный параметр с предварительным или без предварительного [9]. Однако следует учитывать риск чрезмерной параметризации модели путем введения ковариат на основе предположений.
Приоры могут быть реализованы только для ковариантных эффектов. Али и др. . использовал подпрограмму PRIOR для стабилизации только параметров функции созревания (ковариантные эффекты на клиренс) до физиологически правдоподобных значений, поскольку не было данных для детей младше одного года [20]. Аналогичным образом, в своей модели артесуната и дигидроартемизинина PKPD Lohy Das et al. использовали априорные значения для включения эффекта снижения плотности паразитов (, т.е. эффект малярии) на фармакокинетические параметры, поскольку измерения концентрации отсутствовали после первой дозы [21].
Аналогичным образом, в своей модели артесуната и дигидроартемизинина PKPD Lohy Das et al. использовали априорные значения для включения эффекта снижения плотности паразитов (, т.е. эффект малярии) на фармакокинетические параметры, поскольку измерения концентрации отсутствовали после первой дозы [21].
Оценка влияния ковариат, реализованных априори
После априорной реализации влияние ковариат может быть оценено с точки зрения их влияния на параметр, например, графически построив график зависимости параметра от ковариаты [7, 9, 12].Необходимо учитывать физиологическое правдоподобие. Чтобы проверить, существенно ли влияет ковариата на модель в новой популяции, неясно, как можно использовать OFV для сравнения между моделями: LRT нельзя использовать для сравнения моделей напрямую с ∆OFV, когда в информацию PRIOR вносятся изменения. [14].
Крог-Мадсен и др. . выбрал для сравнения OFV по данным (O S ). Две модели, построенные с использованием предшествующей модели (одна с использованием предыдущей модели без ковариаты, а другая с использованием предыдущей модели с одной ковариатой), были запущены на новом наборе данных. Затем их оценки параметров были зафиксированы для запуска тех же двух «настроенных» моделей без повторной оценки (MAXEVAL = 0) на одном и том же наборе данных. OFV сравнивали с помощью LRT. Однако, как указано в разд. 3.3, O S не следует сравнивать между вложенными моделями, если для минимизации OFV использовалась априорная информация.
Затем их оценки параметров были зафиксированы для запуска тех же двух «настроенных» моделей без повторной оценки (MAXEVAL = 0) на одном и том же наборе данных. OFV сравнивали с помощью LRT. Однако, как указано в разд. 3.3, O S не следует сравнивать между вложенными моделями, если для минимизации OFV использовалась априорная информация.
Поиск новых ковариат
Пошаговое ковариатное моделирование
Пошаговое ковариатное моделирование вызывает сомнения при использовании подпрограммы PRIOR. В некоторых статьях ковариаты добавлялись к параметрам, оцененным априорными методами с использованием классического пошагового ковариатного моделирования с прямым включением и обратным удалением (например, p <0.05, то есть порог ∆OFV = 3.84 в гипотезе о том, что ∆OFV имеет хи-квадратное распределение) [5, 19, 23]. На практике следует учитывать особые соображения при поиске ковариат для параметров, которые оцениваются с априорными значениями:
с предварительной информацией о THETA, типичные значения параметров должны быть близки к одному из эталонных моделей: если ковариаты не были одинаково распределены в предыдущей и новой совокупности, ковариата должна быть сосредоточена вокруг ее медианы в предыдущий набор данных.
 В качестве альтернативы можно использовать медианную ковариату нового набора данных, но THETAP должен быть соответствующим образом скорректирован, и важно учитывать, что неопределенность параметра, которая зависит от нормализации, может быть смещена.
В качестве альтернативы можно использовать медианную ковариату нового набора данных, но THETAP должен быть соответствующим образом скорректирован, и важно учитывать, что неопределенность параметра, которая зависит от нормализации, может быть смещена.с предварительной информацией об ETA, введение ковариаты уменьшило бы межличностную изменчивость в меньшей степени, чем если бы межличностная изменчивость оценивалась бы на новом наборе данных.
Насколько это возможно, ковариативный поиск по параметрам модели, оцененным с помощью априорных значений, не должен выполняться: если новые данные статистически слишком слабы, чтобы поддерживать параметр PK / PD, даже на базовой модели, тогда статистическая мощность, вероятно, слишком мала. для поддержки ковариатного анализа по этому параметру.Вместо этого следует искать ковариаты только по параметрам без априорных значений [44]. На первом этапе априорные значения могут быть удалены из всех параметров, которые могут быть оценены без предварительных оценок (см. «Подходы к удалению априорных значений» в разделе 3.2.3). Впоследствии по этим параметрам может быть выполнен ковариативный поиск.
«Подходы к удалению априорных значений» в разделе 3.2.3). Впоследствии по этим параметрам может быть выполнен ковариативный поиск.
Полное ковариатное моделирование
Робби и др. . использовал подход полного ковариатного моделирования [13]. Оценки ковариантных эффектов были изучены в контексте величины эффекта и точности размера эффекта.Ковариаты сохранялись, если 95% доверительный интервал их оценок, полученных с помощью бутстрапа, не включал 1 (что эквивалентно отсутствию эффекта). Подход ковариантного моделирования, в котором упор делался на оценку параметров, а не на пошаговое тестирование гипотез, использовался для этого популяционного PK-анализа, чтобы избежать проблем, связанных с тестом отношения правдоподобия в моделях со смешанным эффектом, включая корреляцию или коллинеарность предикторов, множественные сравнения и искусственная точность параметров.
Валидация модели, построенной с априори
В большинстве рассмотренных статей проверялись модели, построенные с априори, с использованием диагностики на основе моделирования (т. е. VPC [5, 6, 9, 11,12,13,14, 17,18,19,20,21,22,23,24, 28, 30,31,32,33,34], pcVPC [8, 10 , 16, 29] и NPDE [9, 25, 29]). Некоторые использовали бутстрап [4, 5, 9, 11,12,13,14, 16,17,18, 20, 23,24,25, 27, 32, 34], SIR [28] и внешнюю проверку [30, 33 , 34].
е. VPC [5, 6, 9, 11,12,13,14, 17,18,19,20,21,22,23,24, 28, 30,31,32,33,34], pcVPC [8, 10 , 16, 29] и NPDE [9, 25, 29]). Некоторые использовали бутстрап [4, 5, 9, 11,12,13,14, 16,17,18, 20, 23,24,25, 27, 32, 34], SIR [28] и внешнюю проверку [30, 33 , 34].
Важно подчеркнуть, что моделирование с использованием модели, построенной с использованием априорных значений, действительно принимает во внимание априорные факторы для моделирования с неопределенностью. Чтобы моделировать без неопределенности, необходимо отключить априор (который представляет неопределенность параметра совокупности) в настроенной модели.Это выполняется простым удалением априорных значений из файла имитационной модели. Это тот случай, если цель состоит в том, чтобы убедиться, что окончательные оценки адекватно описывают данные. Неопределенность параметров популяции может быть включена для охвата широкого диапазона возможностей, если цель состоит в том, чтобы исследовать все возможные наборы данных, которые могут возникнуть в будущем испытании. Эту функциональность можно использовать на простой модели, построенной без предварительного уведомления, с указанием неопределенности в позициях $ PRIOR.
Эту функциональность можно использовать на простой модели, построенной без предварительного уведомления, с указанием неопределенности в позициях $ PRIOR.
Популяционный физиологически обоснованный PK (popPBPK)
В трех статьях модели, реализованные в качестве априорных, были физиологически обоснованными фармакокинетическими (PBPK) моделями, поскольку они включали два типа входных данных: системные (физиологические) параметры (, например, кровотоки, объемы органов, состав тканей) и параметры, связанные с лекарством ( например, связывание белков плазмы, клиренс и коэффициенты распределения плазмы в ткани (Kp)).
Из этих трех, две были «физиологической моделью ПК всего тела (WBPBPK)» [4, 8], а одна была так называемой «механистической моделью ПК с использованием интегрированного подхода popPBPK» [11], которая включала отсек «остальная часть тела».В этих моделях PBPK параметры, связанные с системой, были фиксированными, поскольку они считались известными на уровне фиксированного эффекта (типичный индивидуальный). Кроме того, параметры, связанные с лекарственными средствами, оценивались априори, поскольку эти параметры были получены из экспериментов in vitro или расчетов in silico и поэтому были связаны с определенной степенью неточности / неточности. В зависимости от модели оценивалась индивидуальная изменчивость клиренса и / или значения (ей) Kp.
Кроме того, параметры, связанные с лекарственными средствами, оценивались априори, поскольку эти параметры были получены из экспериментов in vitro или расчетов in silico и поэтому были связаны с определенной степенью неточности / неточности. В зависимости от модели оценивалась индивидуальная изменчивость клиренса и / или значения (ей) Kp.
По сравнению с полным байесовским анализом в WINBUGS время выполнения было существенно сокращено, а оценки были аналогичными [4].Более того, в отличие от полного байесовского анализа, функция PRIOR позволила оценить некоторые параметры без предварительного уведомления, что удобно, когда априорная информация отсутствует для некоторых параметров модели [11].
Предварительное уведомление об импортируемых пищевых продуктах
Войти / Создать учетную запись
Номер утверждения OMB: 0910-0520
Срок действия OMB: 31.07.2020
См. Заявление о бремени OMB
Закон 2002 года о безопасности общественного здравоохранения и готовности к биотерроризму и ответных мерах (Закон о биотерроризме) предписывает Управлению по контролю за продуктами и лекарствами (FDA) как органу по регулированию пищевых продуктов Министерства здравоохранения и социальных служб предпринять дополнительные шаги для защиты населения. от угрозы или фактического террористического нападения на U.S. поставка продовольствия и другие чрезвычайные ситуации, связанные с продовольствием.
от угрозы или фактического террористического нападения на U.S. поставка продовольствия и другие чрезвычайные ситуации, связанные с продовольствием.
Наряду с другими положениями, Закон требует, чтобы FDA получало предварительное уведомление о пищевых продуктах, включая корма для животных, которые импортируются или предлагаются для импорта в США. Заблаговременное уведомление об импортных поставках позволяет Управлению по контролю за продуктами и лекарствами при поддержке Таможенной и пограничной службы США (CBP) более эффективно направлять инспекции импорта и помогать защищать продовольственные запасы этой страны от террористических актов и других чрезвычайных ситуаций в области общественного здравоохранения.
Закон FDA о модернизации безопасности пищевых продуктов (FSMA), подписанный 4 января 2011 года, направлен на обеспечение безопасности пищевых продуктов в США за счет смещения внимания федеральных регулирующих органов с реагирования на загрязнение на его предотвращение. 5 мая 2011 года FDA опубликовало временное окончательное правило, требующее, чтобы лицо, подавшее предварительное уведомление об импортированных продуктах питания, включая продукты для животных, сообщало название любой страны, в которую было отказано во ввозе данной статьи. Новая информация может помочь FDA принимать более обоснованные решения в управлении потенциальными рисками, связанными с импортом пищевых продуктов в Соединенные Штаты.
5 мая 2011 года FDA опубликовало временное окончательное правило, требующее, чтобы лицо, подавшее предварительное уведомление об импортированных продуктах питания, включая продукты для животных, сообщало название любой страны, в которую было отказано во ввозе данной статьи. Новая информация может помочь FDA принимать более обоснованные решения в управлении потенциальными рисками, связанными с импортом пищевых продуктов в Соединенные Штаты.
Дополнительный обзор и история вопроса
Подача предварительного уведомления
Инструкции по системному интерфейсу предварительного уведомления (PNSI) см. В разделе «Подача предварительного уведомления», который включает следующие и другие ресурсы:
Руководящие документы и правила
Международная почта и подарки
Связаться с FDA
Служба поддержки системы
800-216-7331
240-247-8804 INTL
Обращайтесь по вопросам, касающимся создания учетной записи PNSI, управления, сброса пароля и технических вопросов по компьютеру. (Пн – пт с 7:30 до 23:00 EST)
(Пн – пт с 7:30 до 23:00 EST)
Отдел защиты пищевых продуктов, нацеленный на
(бывший Центр предварительного уведомления)
866-521-2297
571-468-1488 INTL
571-468-1936 Факс
[email protected]
Контакт для вопросов относительно политика, процедуры и интерпретации предварительного уведомления. (24/7)
Отдел импортных операций и политики
301-796-0356
Обращайтесь по вопросам импорта, не связанным с предварительным уведомлением.
Крайние сроки редактирования — Аспирантура
Крайние сроки электронных диссертаций и диссертацийСроки:Электронная диссертация и диссертация (ETD) | Лето2020 | Осень2020 | Весна 2021 г. | Лето 2021 г. |
|---|---|---|---|---|
Начало занятий | 11 мая 2020 | авг. 31 августа 2020 г. ** 31 августа 2020 г. ** | 11 января 2021 г. ** | 10 мая 2021 г. |
Заявление на получение степени | 29 июня 2020 | 25 сентября 2020 г. | 5 февраля 2021 г. ** | 30 июня 2021 г. |
Подача докторских диссертаций | 19 июня 2020 г. ** | 7 октября 2020 г. ** | 10 февраля, 21,2021 | 8 июня 2021 г. |
Подача кандидатских диссертаций | 17 июля 2020 г. ** | окт.28 августа 2020 г. ** | 15 марта 2021 г. | 9 июля 2021 г. |
Окончательная подача (все студенты ETD) | 29 июля 2020 г. ** | 18 ноября 2020 г. ** ** | 1 апреля 2021 г. | 28 июля 2021 г. ** |
Окончательная очистка (утверждение) | 14 августа 2020 г. ** | дек.11 февраля 2020 г. ** | 21 апреля 2021 г. | 4 августа 2021 г. |
Очистить приор(до ближайшего срока) | 28 августа 2020 г. ** | 8 января 2021 г. ** | 7 мая 2021 г. | 20 августа 2021 г. |
** Эти даты были продлены в связи с COVID-19. Для гиперссылки на наши крайние сроки всегда используйте сокращенный бессрочный URL http://graduateschool.ufl.edu/editorial/deadlines.
Этот изнаночный никогда не изменится, даже если прикрепления за ним будут соответствующим образом обновлены.

Диссертация и требования к формату диссертации
Перейдите по этой ссылке, чтобы просмотреть рекомендации по формату диссертаций и диссертаций УФ.
Здесь, http://graduateschool.ufl.edu/graduate-life/graduation/graduation-checklist/, вы найдете полные контрольные списки для дипломных и диссертационных студентов.
Диссертация и диссертация: итоговые процедуры и этапы
Заявление на получение степени
Заявление на получение степени ДОЛЖНО быть подано ДО того, как вы сможете подать документ на рассмотрение в редакцию аспирантуры и до подачи заявления на получение степени в течение предполагаемого срока присуждения степени. Заявки на соискание ученой степени подаются через ONE.UF.
Обратите внимание: в начале срока может возникнуть ошибка «Заявление на получение степени не найдено» даже при наличии действительного заявления на получение степени.Это может происходить до тех пор, пока Отдел документации выпускников не завершит аттестацию по выпускному классу предыдущего семестра. Если вы получили это сообщение об ошибке и отправили заявку на получение степени более 1 рабочего дня назад, отправьте копию своей текущей заявки на ученую степень вместе с диссертацией в формате PDF или диссертационным документом в редакцию аспирантуры по электронной почте на имя выпускника. [email protected], и мы будем рады установить для вас рекорд.
Если вы получили это сообщение об ошибке и отправили заявку на получение степени более 1 рабочего дня назад, отправьте копию своей текущей заявки на ученую степень вместе с диссертацией в формате PDF или диссертационным документом в редакцию аспирантуры по электронной почте на имя выпускника. [email protected], и мы будем рады установить для вас рекорд.
Первая подача докторской диссертации
Это последний день для входа в GIMS, чтобы загрузить полностью отформатированную докторскую диссертацию в формате PDF для просмотра одним из наших редакторов.Диссертация должна быть представлена не позднее 17:00. в этот крайний срок, чтобы продвинуться вперед к получению степени в этом семестре. Все материалы принимаются через Систему управления информацией о выпускниках (GIMS). После входа в GIMS вы увидите ссылку для создания редакционного пакета.
Обратите внимание: Докторанты должны устно защитить свою диссертацию до крайнего срока Final Submission , но не обязаны защищать свою диссертацию до подачи на рассмотрение редакцией First Submission . Хотя это не требуется для защиты перед подачей первой заявки, сопроводительное письмо должно быть отправлено в GIMS академическим подразделением до того, как любой докторант попытается подать свою диссертацию на рассмотрение редакцией в первый раз.
Хотя это не требуется для защиты перед подачей первой заявки, сопроводительное письмо должно быть отправлено в GIMS академическим подразделением до того, как любой докторант попытается подать свою диссертацию на рассмотрение редакцией в первый раз.
Магистерская диссертация Первое представление
Вам необходимо отправить кандидатскую диссертацию в наш офис на рассмотрение, как только вы успешно сдадите устную защиту. После успешной устной защиты ваш департамент должен отправить финальную форму экзамена в SIS.Крайний срок подачи заявок — последний день для входа в GIMS, чтобы загрузить полностью отформатированную магистерскую диссертацию в формате PDF для проверки одним из наших редакторов — не ждите до этого дня, чтобы отправить документ на проверку. Тезисы должны быть отправлены не позднее 17:00. в этот крайний срок, чтобы продвинуться вперед к получению степени в этом семестре. Все материалы принимаются через Систему управления информацией о выпускниках (GIMS). После входа в GIMS вы увидите ссылку для создания редакционного пакета.
После входа в GIMS вы увидите ссылку для создания редакционного пакета.
Обратите внимание: Студенты, получившие степень магистра, должны устно защищаться перед подачей первой заявки в редакцию. Соответственно, для магистрантов окончательные данные экзаменов должны быть отправлены в SIS академическим подразделением студента до того, как студент отправит тезис на рассмотрение редакцией First Submission . Рекомендуется, чтобы как только устная защита прошла успешно, окончательная дата экзамена должна быть опубликована кафедрой, а студент должен незамедлительно отправить диссертацию в редакцию для проверки.Если требуются дополнительные изменения в тезисный документ, назначенное председателем комитета лицо должно удерживать страницу с подписью ETD от размещения в GIMS до тех пор, пока все изменения в тезисный документ не будут внесены к удовлетворению комитета. Страница подписи ETD должна быть размещена в записи студента GIMS к крайнему сроку Final Submission , в пределах предполагаемого срока присуждения степени.
Окончательная подача
Как только страница с подписью ETD будет подписана всем вашим комитетом и размещена в GIMS, вы должны отправить окончательный документ на рассмотрение в наш офис.Не дожидайтесь окончательного срока подачи заявок. Последний срок подачи — последний день, когда вы делаете первую попытку окончательного принятия редакцией Высшей школы. Эта дата применяется только к кандидатам и студентам, которые ранее успешно выполнили срок Первой подачи . Это последний возможный день для подачи окончательного документа на рассмотрение редакции через Систему управления информацией о выпускниках (GIMS). Итоговая диссертация / диссертация должна быть представлена не позднее 17:00.м. в этот крайний срок, чтобы продвинуться вперед к получению степени в этом семестре.
Обратите внимание: После защиты, если требуются дополнительные исправления в диссертации или диссертации, назначенное председателем комитета лицо может удерживать страницу с подписью ETD от размещения в GIMS до тех пор, пока все изменения в документ не будут внесены к удовлетворению комитета. . Однако эта форма должна быть отправлена в студенческий журнал GIMS к крайнему сроку Final Submission в пределах предполагаемого срока присуждения степени.Студенты не могут подать окончательную заявку или получить статус Final Clearance в редакции без формы ETD. Студенты не могут отправить PDF-документ на окончательное рассмотрение в редакцию до тех пор, пока он не будет одобрен их комитетом для публикации и не будет представлена страница с подписью ETD, поскольку после того, как она была принята редакцией, дальнейшие изменения не могут быть разрешены в окончательной редакции. документ.
. Однако эта форма должна быть отправлена в студенческий журнал GIMS к крайнему сроку Final Submission в пределах предполагаемого срока присуждения степени.Студенты не могут подать окончательную заявку или получить статус Final Clearance в редакции без формы ETD. Студенты не могут отправить PDF-документ на окончательное рассмотрение в редакцию до тех пор, пока он не будет одобрен их комитетом для публикации и не будет представлена страница с подписью ETD, поскольку после того, как она была принята редакцией, дальнейшие изменения не могут быть разрешены в окончательной редакции. документ.
Поскольку у сотен студентов такие же дедлайны, наш офис рекомендует подавать заявки как минимум за 7 рабочих дней до истечения всех сроков, чтобы обеспечить достижение поставленной цели.
Окончательный зазор (утверждение)
Это последний день для окончательного утверждения и принятия редакцией Высшей школы.
Обратите внимание: Этот крайний срок применяется только к студентам, которые успешно выполнили как первый, так и последний крайние сроки подачи. Окончательная версия диссертации должна быть принята до 17:00. в этот срок для присуждения степени в этот срок. Проницательные студенты выполняют все требования задолго до этого крайнего срока, чтобы не допустить, чтобы у них не было шанса не закончить обучение в течение предполагаемого срока присуждения степени. Поскольку есть сотни студентов с тем же крайним сроком окончательного утверждения, за которым непосредственно следует сертификация степени, этот срок является твердым.
Окончательная версия диссертации должна быть принята до 17:00. в этот срок для присуждения степени в этот срок. Проницательные студенты выполняют все требования задолго до этого крайнего срока, чтобы не допустить, чтобы у них не было шанса не закончить обучение в течение предполагаемого срока присуждения степени. Поскольку есть сотни студентов с тем же крайним сроком окончательного утверждения, за которым непосредственно следует сертификация степени, этот срок является твердым.
Очистить крайний срок предварительного окончательного утверждения
(для предполагаемой степени в следующем семестре)
Это последний день для окончательного утверждения и принятия редакцией Высшей школы с намерением присуждения ученой степени в течение предстоящего семестра с отказом от требований к регистрации на последний семестр и платы за обучение в этом предстоящем семестре.
Обратите внимание: Этот крайний срок применяется только к студентам, которые успешно выполнили Первого крайнего срока . Студент, возможно, пропустил Final Submission и / или окончательный срок оформления , , однако, в течение первоначально запланированного срока присуждения степени. Предварительная очистка возможна только для студентов диссертаций и диссертаций, которые выполнили все опубликованные крайние сроки для текущего семестра, за исключением Final Submission и / или Final Clearance из редакции аспирантуры.Никакие другие студенты не имеют права.
Студент, возможно, пропустил Final Submission и / или окончательный срок оформления , , однако, в течение первоначально запланированного срока присуждения степени. Предварительная очистка возможна только для студентов диссертаций и диссертаций, которые выполнили все опубликованные крайние сроки для текущего семестра, за исключением Final Submission и / или Final Clearance из редакции аспирантуры.Никакие другие студенты не имеют права.
Clearing Prior разрешает студентам быть освобожденными от регистрации в последний семестр (срок, в котором будет присуждаться степень). Среди прочих требований, включая успешную устную защиту, окончательная диссертация должна быть принята (а не просто отправлена) до 17:00. в этот срок. По этой причине мы рекомендуем подавать документ не менее чем за 7 рабочих дней до крайнего срока оформления.
Учащийся, запрашивающий предварительную очистку, должен соответствовать ВСЕМ из следующих критериев:
- Студент успешно подал заявку на получение степени на текущий семестр в пределах опубликованных сроков, что подтверждено ONE.
 Ст.
Ст. - Учащийся надлежащим образом прошел текущую регистрацию.
- Студент успешно выполнил текущий срок первой подачи диссертации или диссертации, подтвержденный редакцией посредством электронного письма с подтверждением на имя студента и председателя комитета.
- Студент успешно выполнил все остальные требования к степени и административным требованиям в рамках опубликованных крайних сроков для текущего семестра, за исключением окончательной подачи и / или окончательной проверки в редакции аспирантуры.
- Студент завершает работу над диссертацией или диссертацией в редакции аспирантуры. Никакие другие студенты не имеют права.
1758.07 — Карты допуска по отпечаткам пальцев I уровня; определения
41-1758.07 — Карты допуска к отпечаткам пальцев первого уровня; определения41-1758.07. Карты допуска по отпечаткам пальцев уровня I; определения
A. При получении справки о судимости на уровне штата и на федеральном уровне лица, у которого должны быть сняты отпечатки пальцев в соответствии с настоящим разделом, отдел снятия отпечатков пальцев в Департаменте общественной безопасности должен сравнить запись со списком уголовных преступлений, которые препятствуют этому лицу получение карты допуска по отпечатку пальца I уровня. Если в судимости человека нет правонарушений, перечисленных в подразделах B и C данного раздела, отдел снятия отпечатков пальцев выдает лицу карту допуска по отпечатку пальца I уровня.
Если в судимости человека нет правонарушений, перечисленных в подразделах B и C данного раздела, отдел снятия отпечатков пальцев выдает лицу карту допуска по отпечатку пальца I уровня.
B. Лицо, которое подлежит регистрации в качестве сексуального преступника в этом штате или любой другой юрисдикции или которое ожидает суда или которое было признано виновным в совершении или попытке, подстрекательстве, пособничестве или сговоре с целью совершения одного или нескольких из следующих Правонарушениям в этом штате или аналогичным или аналогичным правонарушениям в другом штате или юрисдикции запрещено получать карту допуска по отпечатку пальца I уровня:
1.Сексуальное насилие над уязвимым взрослым.
2. Инцест.
3. Убийство, включая убийство первой или второй степени, непредумышленное убийство и убийство по неосторожности.
4. Сексуальное насилие.
5. Сексуальная эксплуатация несовершеннолетнего.
6. Сексуальная эксплуатация уязвимого взрослого.
7. Коммерческая сексуальная эксплуатация несовершеннолетнего.
8. Коммерческая сексуальная эксплуатация уязвимого взрослого.
9. Торговля детьми в целях сексуальной эксплуатации в соответствии с положениями статьи 13-3212.
10. Жестокое обращение с детьми.
11. Безнадзорность ребенка.
12. Жестокое обращение с уязвимым взрослым.
13. Сексуальное поведение с несовершеннолетней.
14. Приставание к ребенку.
15. Издевательства над уязвимым взрослым.
16. Опасные преступления против детей согласно определению в статье 13-705.
17. Эксплуатация несовершеннолетних при совершении преступлений, связанных с наркотиками.
18. Взятие ребенка с целью проституции в соответствии с разделом 13-3206.
19. Безнадзорность или жестокое обращение с уязвимым взрослым.
20. Торговля людьми с целью сексуальной эксплуатации.
21. Сексуальное насилие.
22. Производство, публикация, продажа, владение и демонстрация непристойных материалов, как предписано в разделе 13-3502.
23.Предоставление несовершеннолетним вредных предметов в соответствии с разделом 13-3506.
24. Предоставление несовершеннолетним вредных предметов посредством интернет-активности в соответствии с разделом 13-3506.01.
25. Непристойное или непристойное общение по телефону с несовершеннолетними в коммерческих целях в соответствии с разделом 13-3512.
26. Выманивание несовершеннолетнего для сексуальной эксплуатации.
27. Вовлечение лиц в занятие проституцией.
28.Вовлечение лиц в целях проституции под ложным предлогом.
29. Привлечение или размещение лиц в доме проституции.
30. Получение заработка проститутки.
31. Принуждение супруга к проституции.
32. Задержание лиц в доме проституции за долги.
33. Содержание или проживание в доме проституции или занятие проституцией.
34.Содействие.
35. Транспортировка лиц с целью проституции, полигамии и сожительства.
36. Изображение взрослого как несовершеннолетнего, как предписано в разделе 13-3555.
37. Допуск несовершеннолетних к публичной демонстрации сексуального поведения в соответствии с положениями статьи 13-3558.
38. Любое уголовное преступление, связанное с содействием правонарушению несовершеннолетнего.
39. Незаконная продажа или покупка детей.
40.Детское двоеженство.
41. Любое уголовное преступление, связанное с насилием в семье, как определено в разделе 13-3601, за исключением уголовного преступления, связанного только с уголовным ущербом на сумму более двухсот пятидесяти долларов, но менее одной тысячи долларов, если преступление было совершено до 29 июня, 2009.
42. Любое уголовное преступление в нарушение раздела 13 главы 12, если оно совершено в течение пяти лет до даты подачи заявления на получение карты проверки отпечатков пальцев уровня I.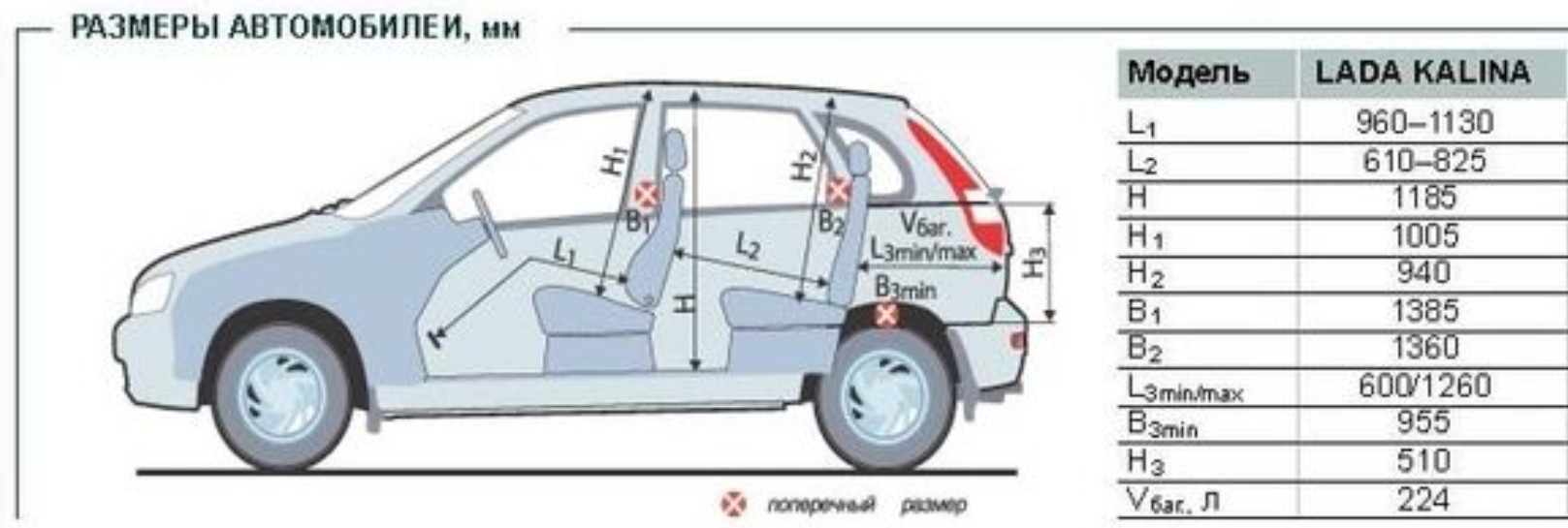
43. Преступления, связанные с наркотиками или алкоголем, если они совершены в течение пяти лет до даты подачи заявления на получение карты проверки отпечатков пальцев уровня I.
44. Непристойное разоблачение тяжкого преступления.
45. Публичное непристойное поведение сексуального характера.
46. Терроризм.
47. Любое преступление, связанное с насильственным преступлением, как определено в разделе 13-901.03.
48. Торговля людьми для принудительного труда или услуг.
C. Лицо, ожидающее суда или признанное виновным в совершении или попытке, подстрекательстве, пособничестве или сговоре с целью совершения одного или нескольких из следующих преступлений в этом штате или таких же или подобных преступлений в другом штате или юрисдикции, не допускается от получения карты допуска к отпечаткам пальцев уровня I, за исключением того, что лицо может подать прошение в комиссию по снятию отпечатков пальцев для исключения уважительной причины в соответствии с разделом 41-619. 55:
55:
1. Любой проступок в нарушение раздела 13 главы 12.
2. Непристойное разоблачение проступка.
3. Мисдиминор публичное непристойное поведение сексуального характера.
4. Уголовный вред при отягчающих обстоятельствах.
5. Воровство.
6. Воровство путем вымогательства.
7. Воровство в магазинах.
8. Подделка.
9. Преступное хранение подделки.
10. Получение подписи обманным путем.
11.Преступное выдача себя за другое лицо.
12. Кража кредитной карты или получение кредитной карты обманным путем.
13. Получение чего-либо ценного, полученного обманным путем с помощью кредитной карты.
14. Подделка кредитной карты.
15. Мошенническое использование кредитной карты.
16. Владение каким-либо оборудованием, пластиной или другим приспособлением или неполной кредитной картой.
17. Ложное заявление о финансовом состоянии или личности для получения кредитной карты.
18. Мошенничество со стороны лиц, уполномоченных предоставлять товары или услуги.
19. Кража записей о транзакциях по кредитной карте.
20. Проступки, связанные с оружием.
21. Неправомерное поведение с использованием взрывчатых веществ.
22. Хранение взрывчатых веществ.
23. Правонарушение, связанное с имитацией взрывных устройств.
24. Нарушение сокрытия оружия.
25. Мелкое хранение и продажа пейота.
26. Хранение пейота и продажа пейота за тяжкое преступление, если оно совершено более чем за пять лет до даты подачи заявления на получение карты проверки отпечатков пальцев уровня I.
27. Проступок при хранении и продажа испаряющегося вещества, содержащего токсичное вещество.
28. Фелоническое хранение и продажа парообразующего вещества, содержащего токсичное вещество, и совершение преступления более чем за пять лет до даты подачи заявления на получение карты разрешения по отпечаткам пальцев уровня I.
29. Мелкая торговля химическими веществами-прекурсорами.
30. Торговля химическими веществами-прекурсорами за совершение тяжкого преступления, если она совершена более чем за пять лет до даты подачи заявления на получение карты проверки отпечатков пальцев уровня I.
31. Незаконное хранение, проступок или продажа марихуаны, опасных или наркотических средств.
32. Хранение, использование или продажа марихуаны, опасных наркотиков или наркотических средств за совершение тяжкого преступления, если оно совершено более чем за пять лет до даты подачи заявления на получение карты разрешения на снятие отпечатков пальцев уровня I.
33. Проступное изготовление или проступок распространение имитации контролируемого вещества.
34. Изготовление или распространение имитационного контролируемого вещества в связи с тяжким преступлением, если оно совершено более чем за пять лет до даты подачи заявления на получение карты проверки отпечатков пальцев уровня I.
35. Мелкое производство или простое распространение имитационного лекарства, отпускаемого только по рецепту.
36. Изготовление или распространение имитационного лекарства, отпускаемого только по рецепту, за совершение тяжкого преступления, если оно совершено более чем за пять лет до даты подачи заявления на получение карточки разрешения на снятие отпечатков пальцев уровня I.
37. Мелкое производство или простое распространение имитации безрецептурного наркотика.
38. Изготовление или распространение имитации безрецептурного наркотика в уголовном порядке, если оно совершено более чем за пять лет до даты подачи заявления на получение карты разрешения по отпечатку пальца уровня I.
39. Проступок или проступок с намерением использовать имитацию контролируемого вещества.
40. Фелоническое владение или хранение с намерением использовать имитацию контролируемого вещества, если оно совершено более чем за пять лет до даты подачи заявления на получение карты разрешения по отпечаткам пальцев уровня I.
41. Незаконное хранение или хранение с намерением использовать имитацию лекарственного средства, отпускаемого только по рецепту.
42. Хранение при тяжком преступлении или хранение с намерением использовать имитацию лекарственного средства, отпускаемого только по рецепту, если оно совершено более чем за пять лет до даты подачи заявления на получение карточки разрешения по отпечаткам пальцев уровня I.
43. Незаконное хранение или хранение с намерением использовать имитацию безрецептурного наркотика.
44.Фелоническое владение или хранение с намерением использовать имитацию безрецептурного наркотика, если оно совершено более чем за пять лет до даты подачи заявления на получение карты разрешения отпечатков пальцев уровня I.
45. Мелкое производство определенных веществ и наркотиков определенными способами.
46. Изготовление определенных веществ и наркотиков определенными способами в уголовном порядке, если оно совершено более чем за пять лет до даты подачи заявления на получение карты проверки отпечатков пальцев уровня I.
47. Добавление яда или другого вредного вещества в еду, питье или лекарства.
48. Уголовное преступление, связанное с преступным посягательством по разделу 13 главы 15.
49. Уголовное преступление со взломом по разделу 13 главы 15.
50. Уголовное преступление по разделу 13 главы 23, за исключением терроризма.
51. Проступки, связанные с безнадзорностью детей.
52. Правонарушения, связанные с правонарушением несовершеннолетнего.
53. Проступки, связанные с насилием в семье, как они определены в статье 13-3601.
54. Уголовные преступления, связанные с насилием в семье, если преступление было связано только с уголовным ущербом в размере более двухсот пятидесяти долларов, но менее одной тысячи долларов, и преступление было совершено до 29 июня 2009 года.
55. Поджог.
56. Уголовные преступления, связанные с продажей, распространением или транспортировкой, предложением продажи, транспортировкой или распространением, или сговор с целью продажи, перевозки или распространения марихуаны, опасных или наркотических средств, если они совершены более чем за пять лет до даты подачи заявления на уровень I карта очистки отпечатков пальцев.
57. Уголовный ущерб.
58. Незаконное присвоение денег чартерной школы в соответствии с положениями статьи 13-1818.
59. Подтверждение личности другого физического или юридического лица.
60. Установление личности другого физического или юридического лица при отягчающих обстоятельствах.
61. Торговля от имени другого физического или юридического лица.
62. Жестокое обращение с животными.
63. Проституция в соответствии с разделом 13-3214.
64. Продажа или распространение материалов, вредных для несовершеннолетних, через торговые автоматы, как указано в разделе 13-3513.
65. Мошенничество в сфере социального обеспечения.
66. Любое уголовное преступление в нарушение раздела 13 главы 12, если оно совершено более чем за пять лет до даты подачи заявления на получение карты проверки отпечатков пальцев уровня I.
67. Похищение.
68. Грабеж, грабеж при отягчающих обстоятельствах или вооруженный разбой.
Д.Лицо, ожидающее суда или осужденное за совершение или попытку совершения мисдиминора, нарушение разделов 28-1381, 28-1382 или 28-1383 в этом штате или такое же или подобное преступление в другом штате или юрисдикции в пределах в течение пяти лет с даты подачи заявления на получение карты контроля отпечатков пальцев уровня I запрещается управлять любым транспортным средством для перевозки сотрудников или клиентов агентства-работодателя в рамках работы данного лица. Отделение должно сделать отметку на карточке допуска по отпечатку пальца I уровня, которая указывает на это ограничение движения.Этот подраздел не запрещает лицу управлять транспортным средством в одиночку в рамках работы по найму.
E. Несмотря на подраздел C этого раздела, после получения письменного уведомления от комиссии по снятию отпечатков пальцев о том, что в соответствии с разделом 41-619.55 было предоставлено исключение по уважительной причине, подразделение по снятию отпечатков пальцев выдает заявителю карту допуска по отпечаткам пальцев уровня I.
F. Если отдел снятия отпечатков пальцев отказывает лицу в подаче заявления на получение карты допуска по отпечатку пальца I уровня в соответствии с подразделом C этого раздела, и запрашивается исключение по уважительной причине в соответствии с разделом 41-619.55, отдел снятия отпечатков пальцев выдает по запросу комиссии по снятию отпечатков пальцев данные о судимости человека в комиссию по снятию отпечатков пальцев.
G. В соответствии с настоящим разделом человеку выдается карта проверки отпечатков пальцев уровня I, если применимо одно из следующих условий:
1. Агентство предоставило исключение по уважительной причине до 16 августа 1999 г., и никаких новых исключающих правонарушений выявлено не было. В карточке допуска по отпечатку пальца должна быть указана только программа, предоставившая исключение по уважительной причине.По запросу заявителя агентство, предоставившее предварительное исключение по уважительной причине, должно уведомить отдел снятия отпечатков пальцев в письменной форме о дате, когда было предоставлено предварительное исключение по уважительной причине, дате осуждения и названии правонарушения, за которое Было предоставлено исключение по уважительной причине.
2. Правление предоставило исключение по уважительной причине, и нового исключающего нарушения не выявлено.
H. Лицензиат или поставщик контракта берет на себя расходы по проверке отпечатков пальцев, проводимой в соответствии с настоящим разделом, и может взимать эти расходы с лиц, у которых требуется снятие отпечатков пальцев.
I. Лицо моложе восемнадцати лет или не менее девяноста девяти лет освобождается от требований, предъявляемых к карточкам для снятия отпечатков пальцев уровня I, установленным в этом разделе. Это лицо должно постоянно находиться под непосредственным визуальным наблюдением персонала, имеющего действующие карты допуска по отпечаткам пальцев первого уровня.
J. Отдел снятия отпечатков пальцев должен проводить периодические проверки судимостей штата и может проводить федеральные проверки криминальных историй, если это разрешено в соответствии с федеральным законом, с целью обновления статуса допуска держателей карт с разрешением по отпечаткам пальцев текущего уровня I в соответствии с данным разделом дактилоскопическая доска и агентство результатов проверки записей.
K. Отдел снятия отпечатков пальцев аннулирует карту допуска отпечатков пальцев уровня I лица при получении письменного запроса об отзыве от комиссии по снятию отпечатков пальцев в соответствии с разделом 41-619.55.
L. Если в судимости человека содержится правонарушение, указанное в подразделах B или C этого раздела, и окончательное решение не записано в протоколе, подразделение должно провести исследование для получения решения в течение тридцати рабочих дней после получения записи. .Если подразделение не может определить в течение тридцати рабочих дней после получения информации о судимости штата и федеральной истории этого лица, ожидает ли лицо суда или было ли оно признано виновным в совершении или попытке, подстрекательстве, пособничестве или сговоре с целью совершения любого из правонарушений перечисленных в подразделах B или C этого раздела в этом штате или при таком же или аналогичном правонарушении в другом штате или юрисдикции, подразделение не выдает лицу карту допуска отпечатков пальцев уровня I.Если подразделение не может принять решение, требуемое этим разделом, и не выдает лицу карту допуска по отпечатку пальца I уровня, это лицо может запросить исключение по уважительной причине в соответствии с разделом 41-619.55.
M. Если после проверки криминальных историй на уровне штата и на федеральном уровне отдел снятия отпечатков пальцев определяет, что он не уполномочен выдавать заявителю карту допуска отпечатков пальцев уровня I, подразделение должно уведомить агентство о том, что отдел снятия отпечатков пальцев не уполномочен выдавать карта допуска по отпечатку пальца уровня I.В этом уведомлении должна быть указана криминальная история, на которой было основано отказ. Эта информация о криминальном прошлом подлежит ограничениям на распространение в соответствии с разделом 41-1750 и публичным законом 92-544.
N. Отдел снятия отпечатков пальцев не несет ответственности за ущерб, причиненный:
1. Выдача карты допуска отпечатков пальцев уровня I заявителю, который, как позже выясняется, не имел права на получение карты допуска отпечатков пальцев уровня I на момент выдачи карты.
2. Отказ в выдаче карты проверки отпечатков пальцев уровня I заявителю, который, как позже выясняется, имел право на получение карты проверки отпечатков пальцев уровня I на момент отказа в выдаче карты.
O. Невзирая ни на какие законы об обратном, физическое лицо может подать заявку и получить карту проверки отпечатков пальцев уровня I в соответствии с этим разделом, чтобы удовлетворить требование о том, чтобы у человека была действующая карта разрешения на отпечатки пальцев, выданная в соответствии с разделом 41-1758.03.
P. Невзирая на любые законы об обратном, за исключением случаев, предусмотренных в соответствии с подразделом Q этого раздела, лицо, которое получает карту проверки отпечатков пальцев уровня I в соответствии с этим разделом, также удовлетворяет требованию о том, чтобы у этого лица была действующая карта разрешения на отпечатки пальцев, выданная в соответствии с к разделу 41-1758.03.
Q. Если владелец карты не совершит правонарушение, указанное в подразделах B или C этого раздела, после 29 июня 2009 г., карта разрешения отпечатков пальцев, выданная в соответствии с разделом 41-1758.03 до 29 июня 2009 г. и его продления действительны для всех требований к карте контроля отпечатков пальцев уровня I, за исключением тех, которые относятся к требованиям разделов 8-105 или 8-509. Карточка допуска по отпечаткам пальцев, выданная до 29 июня 2009 г. в соответствии с требованиями разделов 8-105 или 8-509, и ее продления действительны после 29 июня 2009 г., чтобы соответствовать всем требованиям для карты допуска по отпечаткам пальцев уровня I, включая требования раздела 8-105 или 8-509, если владелец карты был сертифицирован судом для усыновления или получил лицензию на приемную семью до 29 июня 2009 года.
R. Выдача удостоверения личности по отпечаткам пальцев I уровня не дает права на трудоустройство.
S. Для целей данного раздела:
1. «Лицо» означает лицо, у которого взяты отпечатки пальцев в соответствии с:
(а) Раздел 3-314, 8-105, 8-463, 8-509, 8-802, 17-215, 36-207, 36-594.01, 36-594.02, 36-882, 36-883.02, 36 -897.01, 36-897.03, 41-619.52, 41-619.53, 41-1964, 41-1967.01, 41-1968, 41-1969 или 46-141.
(b) Подраздел O этого раздела.
2. «Продление» означает выдачу карты очистки отпечатков пальцев существующему держателю карты очистки отпечатков пальцев, который подает заявку до истечения срока действия существующей карты очистки отпечатков пальцев.
Фармакокинетика дексмедетомидина при длительной инфузии у педиатрических больных в критическом состоянии. Байесовский подход с информативными априорными значениями
В этой работе наличие выбросов в данных было обработано
путем допущения устойчивого t-распределения остатков.
Наш подход отличался от уже представленного
для DEX [37]. В цитируемой работе авторы использовали конечную смесь
в качестве модели остаточной ошибки. Тем не менее, этот конкретный подход
не мог быть использован для нашего набора данных, поскольку он требовал нереалистичного допущения о модели ошибок с аддитивным остатком
и одной модели расположения отсеков.
Персонализированная терапия требует знания
фармакокинетики лекарств и факторов, влияющих на внутрииндивидуальную
вариабельность лекарственного ответа [38].Выяснение
этих факторов кажется особенно важным в педиатрической популяции
, проходящей лечение в отделениях интенсивной терапии интенсивной терапии [39]. Мы думаем, что использование
подхода байесовского вывода могло бы быть эффективным инструментом
для решения часто задаваемых вопросов о
наиболее вероятных различиях между исследуемой популяцией пациентов
и той, которая использовалась для поддержки курса.
парадигма рентного дозирования. Эти вопросы пост-данных часто присутствуют при анализе данных наблюдений и могут эффективно решаться с помощью байесовской теории.
В заключение, популяционная модель PK была успешно разработана для описания динамики и изменчивости
дексмедетомидина у пациентов в ОИТ с использованием аллометрических принципов
и модели созревания клиренса. Статус заболевания, описанный
по шкале PRISM, продолжительность инфузии и пол, не были обнаружены до
, которые не были независимыми значимыми ковариатами в этом исследовании. Наблюдалось увеличение объема распределения
в 1,5 раза после прекращения инфузии
.Были также некоторые свидетельства увеличения клиренса
, однако необходимы дополнительные данные, чтобы полностью подтвердить клиническую значимость этого явления.
Дополнительный материал доступен и включает в себя параметры масс-спектрометрии
, графики кривых параметров модели
по длине цепочки MCMC, подробные сведения о выборе параметров фракции
(f
P
), графики пригодности , Графики ETA, коды
и WinBUGS / Matlab используемых моделей.
Благодарности Этот проект поддержан грантом 2015/17/
B / NZ7 / 03032, основанным Польским национальным научным центром. Мы,
, хотели бы поблагодарить Эмилию Дагир-Войтковяк за ее полезные комментарии
.
Открытый доступ Эта статья распространяется в соответствии с условиями Международной лицензии Creative
Commons Attribution 4.0 (http: // creative
commons.org/licenses/by/4.0/), которая разрешает неограниченное использование, distri-
изготовление и воспроизведение на любом носителе, при условии, что вы предоставите соответствующую ссылку
оригинальному автору (авторам) и источнику, предоставите ссылку на лицензию
Creative Commons и укажете, были ли внесены изменения.
Ссылки
1. Аллегерт К., Олккола К.Т., Оуэнс К.Х., Ван де Велде М., де Маат
М.М., Андерсон Б.Дж. (2014) Варианты внутривенного парацетамола
фармакокинетика у взрослых. BMC Anesthesiol 14:77
2. de Wildt SN (2011) Глубокие изменения в метаболизме лекарств
ферментов и возможное влияние на лекарственную терапию новорожденных и
детей. Мнение эксперта Drug Metab Toxicol. 7: 935–948
3. Smits A, Kulo A, de Hoon JN, Allegaert K (2012) Pharmacoki-
netics лекарств у новорожденных: распознавание образов за пределами конкретных наблюдений соединения
.Curr Pharm Des 18: 3119–3146
4. Hoy SM, Keating GM (2011) Дексмедетомидин: обзор его использования
для седации у пациентов с механической вентиляцией легких в условиях интенсивной терапии и процедурной седации. Наркотики. 71: 1481–
1501
5. Иирола Т., Ихмсен Х, Лайтио Р., Кентала Э, Аантаа Р., Курвинен Дж. П.,
Шейнин М., Швильден Х, Шу
Эттлер Дж., Олккола К.Т. (2012) Поп —
Фармакокинетика дексмедетомидина при длительной седации
у пациентов интенсивной терапии.Br J Anaesth 108: 460–468
6. Alexopoulou C, Kondili E, Diamantaki E, Psarologakis C, Kok-
kini S, Bolaki M, Georgopoulos D (2014) Влияние
дексмедетомидина на качество сна у тяжелобольных пациенты: пилотное исследование
. Anesthesiology 121: 801–807
7. Nelson LE, Lu J, Guo T., Saper CB, Franks NP, Maze M (2003)
Агонист альфа2-адренорецепторов дексмедетомидин сходится на
эндогенном пути, способствующем засыпанию. его успокаивающее
эффектов.Анестезиология 98: 428–436
8. Weinhouse GL, Schwab RJ (2006) Сон у тяжелобольного пациента
. Sleep 29: 707–716
9. Сандерс Р.Д., Сюй Дж., Шу И., Янушевски А., Гальдер С., Фидальго А.,
Сан П., Хоссейн М., Ма Д., Лабиринт М. (2009) Дексмедетомидин
ослабляет изофлуран- индуцированное нейрокогнитивное нарушение у
новорожденных крыс. Анестезиология 110: 1077–1085
10. Мейсон К.П., Лерман Дж. (2011) Обзорная статья: дексмедетомидин у
детей: современные знания и будущие применения.Anesth
Analg 113: 1129–1142
11. Schmidt AP, Valinetti EA, Bandeira D, Bertacchi MF, Simo
˜es
CM, Auler JO (2007) Эффекты преанестетического введения
мидазолама, клонидина или дексмедетомидин при послеоперационной боли
и тревожности у детей. Paediatr Anaesth 17: 667–674
12. Yuen VM, Hui TW, Irwin MG, Yuen MK (2008) Сравнение
дексмедетомидина для интраназального введения и перорального мидазолама для premed-
ication в педиатрической анестезии: двойное слепое рандомизированное исследование
контролируемое исследование.Anesth Analg 106: 1715–1721
13. Sheta SA, Al-Sarheed MA, Abdelhalim AA (2014) Интраназальный
дексмедетомидин против мидазолама для премедикации у детей
, проходящих полную стоматологическую реабилитацию: двойное слепое рандомизированное контролируемое исследование . Paediatr Anaesth 24: 181–189
14. Arcangeli A, D’Alo
` C, Gaspari R (2009) Дексмедетомидин используется для общей анестезии. Curr Drug Targets 10: 687–695
15. Shehabi Y, Botha JA, Ernest D, Freebairn RC, Reade M, Roberts
BL, Seppelt I, Weisbrodt L (2010) Клиническое применение, использование
дексмедетомидина в седация интенсивной терапии.Crit Care Shock.
13: 40–50
16. Tobias JD, Berkenbosch JW (2004) Седация при механической вентиляции легких
у младенцев и детей: дексмедетомидин против
мидазолама. South Med J 97: 451–455
17. Ланн Д. Д., Бест Н., Томас А., Уэйкфилд Дж., Шпигельхальтер Д. (2002)
Байесовский анализ моделей PK / PD населения: общие концепции
и программное обеспечение. J Pharmacokinet Pharmacodyn 29: 271–307
18. Mu S, Ludden TM (2003) Оценка кокинетических параметров популяции pharma-
при несоблюдении.J Phar-
macokinet Pharmacodyn 30: 53–81
19. Gurrin LC, Moss TJ, Sloboda DM, Hazelton ML, Challis JR,
Newnham JP (2003) Использование WinBUGS для установки нелинейных смешанных моделей
с приложением к фармакокинетическому моделированию
ответа инсулина на провокацию глюкозой у овец, подвергшихся воздействию антена-
на глюкокортикоиды. J Biopharm Stat 13: 117–139
20. Stickland MD, Киркпатрик CM, Begg EJ, Duffull SB, Oddie SJ,
Darlow BA (2001) Метод дозирования с увеличенным интервалом для
гентамицина новорожденным.J Antimicrob Chemother 48: 887–893
J Pharmacokinet Pharmacodyn (2016) 43: 315–324 323
123
Содержание предоставлено Springer Nature, применяются условия использования. Права защищены.
Байесовская модель приобретения и устранения бактериальной колонизации, включающая вариации внутри хозяина
Образец цитирования: Ярвенпяя М., Sater MRA, Lagoudas GK, Blainey PC, Miller LG, McKinnell JA и др. (2019) Байесовская модель приобретения и устранения бактериальной колонизации с учетом вариаций внутри хозяина.PLoS Comput Biol 15 (4): e1006534. https://doi.org/10.1371/journal.pcbi.1006534
Редактор: Питер М. Кассон, Университет Вирджинии, США
Поступила: 24.09.2018; Одобрена: 22 февраля 2019 г .; Опубликовано: 22 апреля 2019 г.
Авторские права: © 2019 Järvenpää et al. Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Метод и все соответствующие данные находятся в рукописи и доступны в общедоступном репозитории github (https://github.com/mjarvenpaa/bacterial-colonization-model.git), за исключением распределения расстояний (D_0) который опубликован в другом месте (Gordon N. et al., 2017, Journal of Clinical Microbiology).
Финансирование: PM поддерживается Академией Финляндии (гранты № 286607 и 294015). YHG поддерживается премией Дорис Дьюк в области клинических исследований (2016092).PCB и YHG поддерживаются Национальным институтом аллергии и инфекционных заболеваний США (AI121932). PCB поддерживается премией Career Award в Scientific Interface от фонда Burroughs Wellcome Fund. ГКЛ был поддержан M.I.T. Стипендия Хью Хэмптона Янга и Стипендия для аспирантов Национального научного фонда. Сбор изолятов проводился в рамках гранта (R01HS019388) Агентства по исследованиям и качеству в области здравоохранения. Сбор данных также поддерживается Институтом клинических и трансляционных наук Калифорнийского университета в Ирвине, финансируемым Программой награждения Национальных институтов здравоохранения по клиническим и трансляционным наукам (UL1 TR000153 для SSH).Финансирующие организации не играли никакой роли в дизайне исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Конкурирующие интересы: Авторы заявили, что не существует соответствующих конкурирующих интересов.
Введение
Популяции колонизирующих бактерий часто являются источником заражающих штаммов и передачи новым хозяевам [1–5], поэтому важно понимать динамику этих популяций и факторы, которые способствуют устойчивой колонизации и успеху или неудаче. протоколов клинической деколонизации.Изучение динамики колонизации основано на предположении, представляют ли бактерии из образцов, собранных с течением времени, одну и ту же популяцию или разные события колонизации, что позволяет рассчитать темпы приобретения и удаления [6, 7]. Секвенирование всего генома предоставило подробную меру генетического расстояния между изолятами, которую затем можно использовать для вывода о взаимосвязи между ними [8–11]. Успехи в идентификации передачи и вспышек привели к предложениям о рутинном секвенировании генома клинических и эпиднадзорных изолятов для инфекционного контроля [5, 12].Хотя до настоящего времени в большинстве исследований использовались пороги генетического расстояния в качестве основы для определения взаимосвязи между изолятами [8, 10], здесь мы улучшаем эти эвристические стратегии и представляем надежную и точную полностью байесовскую модель, которая обеспечивает вероятности того, должны ли два штамма быть считается тем же самым, что позволяет нам определять бактериальный клиренс и получение из геномов, взятых с течением времени. Обратите внимание, что здесь мы определяем «штамм» как популяцию близкородственных изолятов.
Пример типичного набора продольно отобранных данных на индивидуальном уровне из исследуемой популяции показан на рис. 1: каждая «строка» представляет пациента, ось x — время, а точки — геномы, отобранные в нескольких временных точках.Цвет точки относится к разным, легко различимым типам последовательностей (ST). Цветное число между двумя последовательными образцами отражает расстояние между геномами, и мы видим, что даже в пределах одного и того же ST расстояния могут значительно различаться, и, следовательно, определение того, можно ли объяснить изменения только эволюцией внутри хозяина, является сложной задачей. Интуитивно, если два генома очень похожи, мы интерпретируем это как один штамм, колонизирующий хозяина, поскольку эти изоляты взяты из близкородственной популяции, проживающей в нише, из которой проводился отбор образцов.С другой стороны, два очень разных генома, даже если один и тот же ST, но с достаточным разнообразием, чтобы последний общий предок проживал за пределами хозяина, интерпретируются как два разных штамма, полученные либо совместно, либо по отдельности как два приобретения. Имея эти данные, мы хотели бы ответить на следующие вопросы: в какой степени люди постоянно колонизируются, очищаются и повторно заселяются? В случае повторного заселения, какова вероятность того, что это тот же или отдельный штамм? Чтобы ответить на эти вопросы, предыдущая работа полагалась на использование порогового количества однонуклеотидных полиморфизмов (SNP) для определения штамма.Оптимально, однако, расстояние SNP между наблюдаемыми геномами и интервал между временем выборки определяет вероятность того, что два генома представляют один и тот же штамм. Такие данные имеют решающее значение для понимания динамики внутри хозяина, реакции на вмешательства и передачи.
Рис. 1. Иллюстрация части данных, использованных в исследовании.
Каждая строка на панели A соответствует одному пациенту. Показаны только первые 20 пациентов. R0 — это первое посещение больницы, а V1, V2 и т. Д.последующие посещения. Красный цвет относится к ST5, а синий — к ST8. Цифры показывают количество мутаций d i между последовательными изолятами. Образцы были получены из мазков из носа и представляют собой отдельные колонии. Пунктирным черным цветом выделены случаи, когда ST изменился с ST 5 на ST 8. На панели B показаны частоты наблюдаемых расстояний d i между последовательными выборками. Эти расстояния использовались для подгонки модели.
https://doi.org/10.1371/journal.pcbi.1006534.g001
Ранее переходы между разными колонизирующими бактериями моделировались с использованием скрытых марковских моделей [13], состояния которых соответствуют различным колонизирующим ST. Однако этот подход не подходит для моделирования в рамках одного ST, где приобретение и клиренс должны определяться на основе небольшого количества мутаций. Решающее значение для интерпретации таких небольших различий имеет модель вариации внутри хозяина [8, 14], определяющая количество мутаций, ожидаемых эволюцией внутри хозяина.Генетические модели популяций могут быть использованы для понимания изменчивости в эволюционирующей популяции [15]. Основная трудность при подгонке таких моделей к данным, подобным показанным на рисунке 1, заключается в том, что информация, содержащаяся в данных, чрезвычайно ограничена в отношении вариаций внутри хозяина: один момент времени суммируется только с одним (или несколькими) геномами, и должны служить для представления всего населения в пределах принимающей стороны. Хотя в некоторых исследованиях используется последовательность генома из нескольких изолятов для достижения более полной характеристики разнообразия внутри хозяина [3, 10], они имеют тенденцию быть ограниченными с точки зрения количества временных точек и / или пациентов.
Байесовская статистическая структура может использоваться для объединения информации из нескольких источников данных. В байесовском подходе априорное распределение обновляется с использованием законов вероятности до апостериорного распределения в свете наблюдений, и это может повторяться несколько раз с разными наборами данных [16, 17]. Приближенное байесовское вычисление (ABC) особенно полезно с популяционно-генетическими моделями, где функцию правдоподобия сложно указать явно, но моделирование модели не вызывает затруднений [18, 19].ABC недавно был введен в популяционную генетику бактерий [20–23]. Здесь мы представляем байесовскую модель для определения того, следует ли рассматривать два генома как один и тот же штамм, что позволяет стратегии, основанной на популяционной генетике, делать выводы о приобретении и удалении из данных близкородственных геномов. Преимущества полностью байесовского анализа включают в себя: точную количественную оценку неопределенности, четкое изложение предположений моделирования (открытое для критики и дальнейшего развития при необходимости) и прямое использование нескольких источников данных.Мы демонстрируем эти преимущества, анализируя большую коллекцию продольно собранных метициллин-устойчивых геномов Staphylococcus aureus (MRSA), полученных в ходе клинических испытаний (Project CLEAR) для оценки эффективности протокола деколонизации MRSA [24]. Этот метод идентификации штаммов с явной оценкой неопределенности позволит изучить характеристики — как хозяина, так и патогена — которые влияют на колонизацию при наличии и отсутствии вмешательств.
Методы
Сбор изолятов и полногеномное секвенирование
изолята MRSA были собраны в рамках клинического исследования Project CLEAR (Изменение жизни путем искоренения устойчивости к антибиотикам) (ClinicalTrials.gov identifier: NCT01209234), разработанный для сравнения воздействия протокола долгосрочной деколонизации на носительство MRSA с обучением пациентов общей гигиене и самообслуживанию [24]. Субъекты исследования были набраны из госпитализированных пациентов на основании положительной культуры MRSA или мазка для наблюдения. После набора из носа у субъектов были взяты мазки из носа примерно во время выписки из больницы (R0) и через 1,3,6 и 9 месяцев (V1-V4, соответственно) после получения первоначального образца. Были включены только эти образцы, полученные в рамках клинического исследования.Обратите внимание, что у некоторых включенных в исследование субъектов, несмотря на колонизацию или инфекцию MRSA в анамнезе, мазки не были положительными на MRSA в первый момент времени (R0).
Мазки культивировали на хромогенном агаре, и отдельные колонии отбирали из полученного роста. Библиотеки парных концевых ДНК были созданы с помощью Illumina Nextera в соответствии с инструкциями производителя. Библиотеки секвенировали на платформе Illumina Hiseq. Считывания секвенирования были собраны de novo с использованием SPAdes-3.10.1 [25], а соответствующий тип последовательности (ST) и клональный комплекс (CC) были определены путем сопоставления с базой данных PubMLST (https: // pubmlst.org / saureus /) и eBURST (http://saureus.mlst.net/eburst/). Считывания секвенирования были картированы с использованием BWA mem v0.7.12 [26]. Для изолятов CC8 и CC5 чтения были сопоставлены с TCh2516 (GenBank ID CP000730.1) и Jh2 (CP000736.1) соответственно. Повторяющиеся чтения были отмечены инструментами Picard V2.8.0 (http://broadinstitute.github.io/picard/) и проигнорированы. Вызов SNP производился с использованием параметров по умолчанию Pilon [27]. Области с низким охватом (<10 считываний) или неоднозначными вариантами неоднозначного картирования были отброшены.Области с повышенной плотностью SNP, представляющие предполагаемые события рекомбинации или фаг, как определено Gubbins v2.3.3 [28], также были отброшены. Считывания секвенирования можно найти в NCBI SRA, доступ PRJNA224550.
Обзор модели
Один элемент входных данных для нашей модели состоит из пары геномов, которые относятся к одному и тому же ST, взятых у одного и того же человека в двух последовательных временных точках (или, возможно, с промежуточным моментом времени без образцов или выборкой другого ST) .Каждый из этих элементов данных (то есть пары последовательных геномов) суммируется с точки зрения двух величин: расстояния между геномами и разницы между их временами выборки (см. Рис. 1). Следовательно, наблюдаемые данные D можно записать как состоящие из пар ( d i , t i ), i = 1,…, N , где t i > 0 — время между выборкой геномов, d i ∈ {0, 1, 2,…} — наблюдаемое расстояние, а N — общее количество генома пары, удовлетворяющие критериям (т.е. тот же пациент, тот же ST, последовательные моменты времени или, возможно, с промежуточным моментом времени без образцов или образец другого ST). Ограничение пар геномов одного и того же ST проистекает из того факта, что разные ST в любом случае всегда будут считаться разными штаммами. Можно включить несколько геномов, отобранных в один и тот же момент времени, при условии некоторого упорядочения (например, случайного) и установки t i равным нулю, но модель, специально разработанная для этого, описана в разделе ABC. предварительное использование внешних данных.
Есть два возможных объяснения наблюдаемых расстояний. Если геномы принадлежат к одному штамму, мы ожидаем, что расстояние между ними будет относительно небольшим. Если геномы принадлежат к разным штаммам, мы ожидаем большего расстояния. Ниже мы определяем две вероятностные модели, которые представляют эти два альтернативных объяснения. Затем эти модели объединяются в одну общую модель смеси, которая предполагает, что расстояние между определенной парой геномов генерируется либо из модели «одного штамма», либо из модели «другого штамма», и позволяет рассчитать вероятности этих двух альтернатив. для каждой пары геномов, а не полагаться на фиксированный порог, чтобы различать их.
Неотъемлемой частью нашего подхода является популяционно-генетическое моделирование, которое позволяет нам моделировать вариации внутри хозяина и, следовательно, делать вероятностные утверждения о правдоподобности моделей «одного и того же штамма» по сравнению с «разными штаммами». Для этой цели мы принимаем общую имитационную модель Райта-Фишера (WF), см., Например, [29], с постоянной частотой мутаций и размером популяции, которые оцениваются по данным. Моделирование начинается с того, что все геномы одинаковы, что соответствует биологическому сценарию, согласно которому колонизация начинается с быстрого размножения одного изолята до достижения максимальной «емкости» с последующей медленной диверсификацией популяции.Это предположение подтверждается тем фактом, что в распределении расстояний, в случаях, когда время сбора данных было известно и произошло недавно, наблюдались очень незначительные вариации в популяции. См. Раздел «Обсуждение» для получения более подробной информации о предположениях моделирования. Обзор подхода, включая наборы данных, модели и методы вывода, представлен на рис. 2 и подробно обсуждается ниже.
Рис. 2. Обзор шагов моделирования и подбора данных.
На этапе 1 мы обновляем нашу предварительную информацию о параметрах ( n eff , μ ) на основе внешних данных D 0 .На этапе 2 мы оцениваем все параметры (смешанной) модели с использованием MCMC, предварительно вычисленных распределений расстояний p S и информации, полученной на этапе 1. Подобранная модель может использоваться, например, для получить такую же вероятность деформации для нового (будущего) измерения.
https://doi.org/10.1371/journal.pcbi.1006534.g002
Модель
p S : Та же деформация.Пусть ( s i 1 , s i 2 ) обозначает пару геномов на расстоянии d i , взятых у пациента в двух последовательных временных точках ( см. предыдущий раздел) со временем t i между взятием проб.Здесь мы представляем модель, т.е. распределение вероятностей p S ( d i | t i , n eff , μ ), который сообщает, какие расстояния нам следует ожидать, если геномы принадлежат к одному штамму, т.е. представляют собой близкородственную популяцию, которая эволюционировала в результате одного события колонизации. Параметр n eff — это эффективный размер популяции, а μ — частота мутаций.Мы моделируем d i как (1) где мы определили (2) где dist (⋅, ⋅) — это функция расстояния, которая сообщает количество мутаций между ее аргументами, а s i * — уникальный предок s i 2 , который присутствовал в хозяин, когда был взят образец s i 1 , который произошел внутри хозяина от того же генома, что и s i 1 (см. рис. 3A).Уравнение 1 действительно, когда произошли мутации между s i 1 и s i * и s i * и s i 2 в разных сайтах, что с большой вероятностью верно, когда геномы длинные (миллионы бит в секунду) по сравнению с количеством мутаций (десятки или несколько сотен максимум). Распределение вероятностей d i 1 , которое мы обозначим p sim ( d i 1 | n eff , μ ), и которое недоступен аналитически и не зависит от t i , представляет собой вариацию внутри хоста в один момент времени.Мы аппроксимируем это как (3)
Рис. 3. Схема моделей «одинаковой деформации» и «разной деформации».
Модель p D слева (панель A) представляет ситуацию, когда геномы, обозначенные как s i 1 и s i 2 , относятся к одному штамму . Модель p S справа (панель B) показывает случай, когда эти геномы принадлежат к разным штаммам.На рисунках время течет слева направо, точки представляют индивидуальные геномы, а края — отношения между родителями и потомками.
https://doi.org/10.1371/journal.pcbi.1006534.g003
Предполагается, что распределение d i 2 (4) то есть предполагается, что мутации происходят в соответствии с процессом Пуассона с параметром скорости µ , что следует из предположения о постоянной скорости мутаций в модели Райта-Фишера.
Модель
p D : Различные деформации.Модель p D представляет собой случай, когда геномы s i 1 и s i 2 относятся к разным штаммам, что, по нашему определению, означает, что их самые последние общий предок (MRCA), обозначенный s iA , находился вне хоста. Время между с iA и с i 1 обозначено как t 0 i (см. Рис. 3B).В модели p D мы предполагаем, что распределение расстояния d i равно (5) где значения t 0 i неизвестны и будут оценены, но пока предположим, что они известны. Одно различие между одной и той же моделью деформации p S (определяется уравнениями 1, 3 и 4) и другой моделью деформации p D (уравнение 5) заключается в том, что в первой модели используется метод Райта-Фишера. моделирование, тогда как последнее — нет.Причина в том, что вариации внутри хозяина ограничены, иногда увеличиваясь и уменьшаясь, что отражается постоянным размером популяции при моделировании Райта-Фишера в той же модели деформации. В другой модели деформации расстояние между s i 1 и s i 2 может в принципе неограниченно увеличиваться, если прошло достаточно времени с момента их общего предка, потому что они расходились и развивались за пределами хозяин.
Модель смеси.
С двумя альтернативными моделями расстояния мы можем написать полную модель, которая предполагает, что каждое наблюдение расстояния распределено в соответствии с (6) где θ обозначает вместе все параметры моделей, т. е. θ = ( n eff , μ , ω S , ω D , т 01 ,…, т 0 N ).Параметр ω S представляет долю пар из одной и той же деформации, а ω D представляет собой долю пар из разных деформаций, так что ω S + ω D = 1. Чтобы узнать неизвестные параметры θ , нам нужно подогнать модель к данным, но прежде чем вдаваться в подробности, мы обсудим, как использовать внешний набор данных для обновления предыдущего распределения о частота мутаций μ и эффективный размер выборки n eff .Это обновленное распределение будет само использоваться как предыдущее в модели смеси.
Вывод ABC для обновления предыдущего с использованием внешних данных
Моделирование с помощью модели WF используется в нашем подходе для двух целей: 1) для включения информации из внешнего набора данных для обновления предшествующего значения частоты мутаций μ и эффективного размера выборки n eff , и 2 ), чтобы эмпирически определить распределение p S ( d i | t i , n eff , μ ), необходимое в модели смеси.Здесь мы обсуждаем первую задачу.
В качестве внешних данных мы используем измерения восьми пациентов, колонизированных MSSA [3], включающие мазки из носа из двух временных точек для каждого пациента, так что, как известно, получение произошло приблизительно непосредственно перед первым мазком. Множественные геномы были секвенированы из каждого образца, и распределения попарных расстояний между геномами обеспечивают моментальные снимки изменчивости внутри хозяина в двух временных точках для каждого человека, и эти распределения расстояний используются в качестве данных.То есть, в отличие от данных D (которые представляют собой расстояния SNP между отдельными изолятами, собранными в разные моменты времени), используемых для соответствия модели смеси, здесь мы используем распределение расстояний SNP в каждой временной точке. Мы исключаем одного пациента (номер 1219), потому что, согласно [3], этот пациент, вероятно, был инфицирован задолго до первого образца. Набор данных также содержит наблюдения еще 13 пациентов из [14], обозначенных буквами от A до M в [3]. Для этих пациентов доступны распределения расстояний только для одной временной точки, а время сбора данных неизвестно.Данные, включающие распределение расстояний от 7 пациентов (две точки времени) и дополнительных 13 пациентов (одна точка времени), совместно обозначены как D 0 .
Чтобы узнать о неизвестных параметрах n eff и μ , сначала отметим, что их значения влияют на распределение расстояний в популяции, полученное в результате моделирования W-F с заданными значениями (рис. 4). Чтобы оценить эти параметры, мы пытаемся найти для них такие значения, которые делают выходной сигнал WF похожим на наблюдаемое распределение расстояний D 0 .Поскольку соответствующая функция правдоподобия недоступна, стандартные статистические методы подгонки модели не применяются. Поэтому мы используем приближенное байесовское вычисление (ABC), класс методов для байесовского вывода, когда вероятность недоступна или слишком дорога для оценки, но моделирование модели возможно, см. [18, 19, 30, 31] для обзора ABC. Базовый алгоритм сэмплера отклонения ABC для подгонки модели состоит из следующих шагов:
- Смоделируйте вектор параметров ( n eff , μ ) из предыдущего распределения p ( n eff , μ ).
- Сгенерируйте псевдоданные, аналогичные наблюдаемым данным D 0 , запустив модель W-F отдельно для каждого пациента с помощью параметра ( n eff , μ ).
- Примите параметр ( n eff , μ ) в качестве выборки из (приблизительного) апостериорного распределения, если расхождение между наблюдаемыми и смоделированными данными меньше заданного порога ε .
Рис 4.Распределение попарных расстояний для популяций, смоделированных с разными параметрами.
Гистограммы показывают оценочные функции массы вероятности с выбранными векторами параметров ( n eff , μ ). Увеличение μ и / или n eff имеет тенденцию к увеличению расстояний. Каждая гистограмма представляет изменчивость в моделируемой популяции в один момент времени через 6000 поколений после начала моделирования.
https: // doi.org / 10.1371 / journal.pcbi.1006534.g004
Качество результирующей аппроксимации ABC зависит от выбора функции невязки, порога ε и количества принятых выборок. Вообще говоря, если расхождение суммирует информацию в данных полностью (например, это функция достаточной статистики) и ε произвольно мало, ошибка аппроксимации становится незначительной, и выборки генерируются на основе точных апостериорных данных. На практике выбор ε очень маленьким делает алгоритм неэффективным, поскольку требуется много моделирования для получения принятой выборки даже с оптимальным значением параметра.Кроме того, найти хорошую функцию несоответствия может быть сложно, потому что обычно нет достаточной статистики. Существует множество сложных вариантов ABC, см., Например, [19, 31] и ссылки в них, но поскольку нам нужно оценить только два параметра (один из которых является дискретным) и поскольку запуск моделирования параллельно с базовым алгоритмом, мы используем выборку отклонения ABC, описанную выше, с подробностями, обсуждаемыми ниже.
В [14] эволюция MRSA была смоделирована с использованием параметров, полученных из следующих оценок: 8 мутаций на геном в год и продолжительность поколения 90 минут (таким образом, весь год составляет 5840 поколений).Это дает частоту мутаций 0,0019 на геном на поколение, приблизительно 6,3 × 10 -10 мутаций на сайт на поколение, при условии, что длина генома составляет 3 Мбит / с. Мы также используем время генерации 90 минут, первоначально полученное [14] из расчетного времени удвоения Staphylococcus aureus [32]. Мы используем независимые равномерные априорные значения для параметров модели WF, так что (7) с a μ = 0,00005 и b μ = 0.005 мутаций на геном на поколение.
Мы утверждаем, что разумные параметры должны давать популяции с аналогичными гистограммами попарных расстояний по сравнению с наблюдениями в соответствующие моменты времени. Следовательно, мы используем невязку Δ, определяемую как (8) где и — смоделированные и наблюдаемые эмпирические распределения попарных расстояний для пациента i с моментом времени t соответственно, а l 1 (⋅, ⋅) обозначает L 1 расстояние между распределениями (альтернативные меры расстояния обсуждаются в дополнительном материале).Обратите внимание, что во втором члене в уравнении 8 мы используем минимум вместо суммирования. Причина в том, что время сбора данных для 13 пациентов (A-M) неизвестно, и их точная оценка была бы невозможной. Вместо этого мы используем эти данные, чтобы заменить неизвестное время значениями, которые производят минимальное расхождение. Таким образом, параметры, которые никогда не дают достаточной изменчивости, чтобы соответствовать наблюдениям, увеличивают расхождение, позволяя нам получить доказательства против таких необоснованных значений, даже если точное время неизвестно и требует слишком больших вычислительных затрат, чтобы сделать вывод.
Вместо моделирования ( n eff , μ ) выборок из предыдущего мы выполняем эквивалентные вычисления на основе сетки. То есть мы рассматриваем равноудаленную сетку 50 × 50 значений ( n eff , μ ) и моделируем модель 1000 раз в каждой точке сетки. Однако в предварительных экспериментах мы заметили, что если n eff и μ одновременно велики, количество мутаций, производимых моделью, быстро увеличивается, и ясно, что смоделированные попарные расстояния всегда больше, чем в наблюдаемых данных. , а также время вычислений и использование памяти становятся недопустимыми.Таким образом, мы не запускаем полный набор из 1000 симуляций в этой области параметров, потому что ясно, что апостериорной плотностью можно пренебречь. Наконец, порог ε выбран так, чтобы 5 000 из общего числа почти 1 миллиона имитаций были ниже порога, что соответствует вероятности принятия 0,0057.
Подробная информация о модели смеси
Теперь мы подробно обсудим модель смеси, а затем выведем эффективный алгоритм для оценки ее параметров.Поскольку значения t 0 i в уравнении 5, обозначающие времена MRCA в случае, если последовательности представляют собой разные штаммы, неизвестны, мы моделируем их как случайные величины и даем каждой из них априорное распределение. (9)
Далее мы укажем слабо информативный априор для λ такой, что (10)
Таким образом, параметр λ распределяется между разными t 0 i , что позволяет нам узнать о его распределении.
Если k = 1, то гамма-распределение в уравнении 9 сводится к экспоненциальному, что, однако, не отражает наше предыдущее понимание разумного значения t 0 i , потому что режим результирующего распределения равен нулю, что соответствует очень недавнему общему предку для геномов, которые, как считается, происходят от разных штаммов.Вместо этого мы устанавливаем k = 5, α = 2,5 и β = 1600, что приблизительно соответствует среднему значению и стандартному отклонению для 5800 и 8400 поколений соответственно. Этот слабо информативный априор отражает представление о том, что разные штаммы расходились в среднем примерно год назад, но с большим разбросом. Кроме того, если время между выборками, t i , составляет три месяца, предварительное значение преобразуется в ожидание, что, если выбранные геномы принадлежат к разным штаммам, они в среднем содержат 30 мутаций с большим стандартом. отклонение 50 мутаций.Более того, у плотности есть тяжелый хвост, чтобы учесть некоторые, возможно, гораздо большие расстояния. Формулы, используемые для вычисления этих значений, и другие полезные факты об априорном, приведены в дополнительном материале.
Эквивалентный способ записи модели смеси в уравнении 6, который также упрощает вычисления, состоит в том, чтобы ввести скрытые метки, которые определяют компонент, который генерировал каждое наблюдение d i , см. [33]. Таким образом, мы определяем скрытые переменные (11)
Априорная плотность для скрытых переменных z равна
(12)
где мы использовали векторные обозначения t = ( t 1 ,…, t N ) T , d = ( d 1 ,…, d N ) T , z = ( z 1 ,…, z N ) T , t 0 = ( т 01 ,…, т 0 N ) T и ω = ( ω S , ω 09 D
09 D
09 D )
Т .Мы увеличиваем параметр θ , чтобы представить вместе все параметры модели в уравнении 6 и априорные плотности, указанные в уравнениях 9 и 10, то есть θ = ( n eff , μ , ω , z , t 0 , λ) T . Чтобы завершить спецификацию модели, мы должны указать предшествующие для ω , n eff и μ .Мы используем
(13)
то есть распределение Дирихле с параметром γ = (1, 1) T . Мы используем апостериорный p ( n eff , μ | D 0 ), полученный ABC с использованием внешних данных D 0 , как обсуждалось в предыдущем разделе, как ( стык) до ( n eff , μ ).
Байесовский вывод для модели смеси
Теперь мы покажем, как модель смеси может эффективно соответствовать данным.Совместное распределение вероятностей для данных d и параметров θ теперь можно записать как (14) (15)
Мы используем выборку Гиббса, которая представляет собой алгоритм MCMC, для выборки из апостериорной плотности. Алгоритм использует иерархическую структуру модели и выполняет итеративную выборку из условной плотности каждой переменной (или блока переменных) за раз [34]. Далее мы выводим условные плотности для алгоритма выборки Гиббса.Мы заметили, что некоторые из параметров θ сильно коррелированы, что вызывает медленное перемешивание результирующей цепи Маркова и, следовательно, неэффективное исследование пространства параметров. Чтобы сделать алгоритм более эффективным, мы повторно параметризуем модель, задав новые параметры θ ′ = ( n eff , μ , ω , z , η , λ) через преобразование η = μ t 0 , и мы используем семплер Гиббса для преобразованных параметров θ ′.Эта общая стратегия [34] решает проблему, возникающую из-за корреляций между t 0 i и μ , потому что величины всех η i теперь могут быть изменены одновременно с помощью одного μ. обновление. Исходные переменные t 0 i могут быть получены из сгенерированных выборок как t 0 i = η i / μ .
Совместная вероятность в уравнении 15 для преобразованных параметров тогда становится равной (16) где μ — N — определитель якобиана обратного преобразования. Вычислить условную плотность параметра ω просто. Мы пренебрегаем теми членами в уравнении 16, которые не зависят от ω , и признаем полученную формулу ненормализованным распределением Дирихле. Тогда получаем (17) с n = ( n 1 , n 2 ) T , где и.Далее мы рассматриваем скрытые переменные z i . Мы видим, что условное распределение z i для любого i = 1,…, N не зависит от других скрытых переменных z j , j ≠ i . В частности, получаем (18) (19)
Мы ожидаем, что эффективный размер выборки n eff и параметр мутации μ будут коррелированы апостериори, поэтому мы включаем их в один и тот же блок и обновляем их вместе.Мы также включаем λ в этот блок, поскольку он также имеет тенденцию коррелировать с n eff и μ . Шаг выборки удобно заменить на p ( n eff , μ , λ | ω , z , η , D , D 0 ) со следующими двумя последовательными шагами выборки: первая выборка из p ( n eff , μ | ω , z , η , D , D 0 ) = ∫ p ( n eff , μ , λ | ω , z , η , D ,
Вышеупомянутая формула признана пропорциональной гамма-плотности как функции λ. Таким образом, мы можем легко маргинализировать λ, чтобы получить следующую плотность для первого шага (21)
На втором этапе мы выбираем λ из плотности вероятности (22)
Эта формула следует непосредственно из уравнения 20.
Выборка из уравнения 21 и выборка z с использованием уравнения 18 являются сложной задачей, потому что p S определяется неявно через имитационную модель WF.Следовательно, мы рассмотрим приближение, которое позволяет вычислить p S ( d i | t i , n eff , μ ) для любая предложенная точка ( n eff , μ ) и все значения d i и t i в данных. Поскольку d i = d i 1 + d i 2 , мы можем использовать формулу свертки для суммы дискретных случайных величин, чтобы увидеть, что (23) где p sim определяет распределение расстояния между двумя геномами, как в уравнении 3, и d m — максимальное расстояние, которое может быть получено из p sim .
Поскольку p sim ( d i 1 | n eff , μ ) не доступен аналитически, мы оцениваем эту функцию массы вероятности путем моделирования. Особым случаем является то, что мы знаем, что во время взятия первой выборки нет изменений в генеральной совокупности s i 1 , что может произойти, если мы знаем, что сбор данных произошел непосредственно перед первой выборкой. В этом случае d i 1 = 0, и нам не нужна симуляция.Поскольку обычно это не так, мы используем следующее общее решение: для каждого значения ( n eff , μ ) мы производим независимую выборку путем моделирования модели WF, отбираем образцы пары геномов в фиксированное время. t из моделируемой популяции и вычислите их расстояние. Это повторяется для j = 1,…, s . Поскольку d i 1 дискретно, мы приближаем (24) для всех и . Поскольку в данных D мы не знаем время сбора данных, мы устанавливаем t = 6000 поколений и используем это же значение для всех i .Это большое значение представляет собой устойчивое состояние моделирования, при котором вариация в популяции иногда увеличивается и уменьшается по мере появления новых линий и отмирания старых, что можно рассматривать как соответствующее разумным ожиданиям по умолчанию в отношении изменчивости популяции, когда истинное время сбора неизвестно. Хотя это предположение было введено для вычислительной необходимости, его можно оправдать, учитывая его влияние на выводы: упрощение может привести к слегка завышенным значениям расстояний d i 1 , если в действительности многие измерения произошли совсем недавно.Следствием этого является то, что критерий для сообщения о новых приобретениях становится более консервативным , потому что теперь модель «одного и того же штамма» будет размещать некоторую вероятностную массу на случайных больших расстояниях и, следовательно, лучше приспосабливать также удаленные геномы, которые в противном случае могли бы рассматриваться как разные штаммы. .
Некоторые из результирующих функций вероятности и массы уже были показаны на рис. 4. На практике вычисления, приведенные выше, выполняются с использованием логарифмов и факта, чтобы избежать потери числового значения, которое может произойти всякий раз, когда a i ≪ 0.Конечный размер выборки s вызывает некоторую числовую ошибку, но, поскольку расстояния обычно достаточно малы, чтобы количество значений, которые нам нужно учитывать, ограничено, s можно сделать достаточно большим без слишком обширных вычислений, что делает эту ошибку небольшой в общем. Вышеупомянутая процедура позволяет вычислить условную плотность в уравнении 21 для любого ( n eff , μ ), и мы можем использовать обновление Metropolis для ( n eff , μ ).Мы исключили λ в уравнении 21, чтобы улучшить перемешивание цепочки и иметь возможность использовать аналитическую формулу в уравнении 22, а в дополнительном материале мы обосновываем, что этот алгоритм действителен в предположении, что новый параметр λ выбирается только в том случае, если соответствующее предложенное значение ( n eff , μ ) было принято.
Всякий раз, когда предлагается новый ( n eff , μ ) -параметр, нам нужно вычислить p sim на этом этапе, чтобы проверить условие приемки.Это значение также необходимо при выборке z . Однако вычисление p sim на каждой итерации MCMC, как описано ранее, делает алгоритм медленным. Следовательно, вместо этого мы предварительно вычисляем значения p sim в плотной сетке ( n eff , μ ) -точек, что может быть выполнено параллельно на компьютерном кластере. Учитывая значения сетки, мы используем билинейную интерполяцию для аппроксимации p sim в каждой предложенной точке.Аналогично поступаем и с априорной плотностью p ( n eff , μ | D 0 ). Этот подход также позволяет подобрать модель смеси с использованием различных допущений моделирования или разных наборов данных без необходимости повторять дорогостоящие модели W-F.
Наконец, мы видим, что плотность вероятности η i , обусловленная другими переменными, не зависит от η j , j ≠ i .В частности, получаем (25) для i = 1,…, N . Вывод этого результата, формула для весов смеси w j и специальный алгоритм (алгоритм 2) для генерации случайных значений из этой плотности показаны в дополнительном материале.
Получившийся в результате сэмплер Гиббса представлен как алгоритм 1. Его можно также назвать сэмплером Метрополиса внутри Гиббса, поскольку некоторые из параметров ( n eff и μ ) отбираются с использованием шага Метрополиса-Гастингса с плотность предложения, которая обозначается как q .Поскольку n eff — дискретная случайная величина, ( n eff , μ ) — смешанный случайный вектор, и мы не можем использовать стандартное предложение Гаусса. Вместо этого мы рассматриваем распределение (26) где и выбраны для получения вероятности принятия шага Метрополиса, близкой к 0,25, а δ (⋅) — дельта-функция Дирака. Первый элемент случайной выборки из q в уравнении 26 является целым числом, и это предложение также является симметричным.Мы усекаем хвосты q относительно n eff , чтобы иметь возможность эффективно отбирать дискретный элемент из q . На практике мы затем используем предложение q , которое представляет собой плотность смеси, в которой компоненты такие же, как в уравнении 26, но с другими параметрами дисперсии, и иногда предлагаем большие шаги для увеличения исследования пространства параметров.
Алгоритм 1 Алгоритм выборки MH-в-Гиббса для модели смеси
выберите начальный параметр θ ′ (0) (e.грамм. путем выборки из предшествующего p ( θ ′)), предложения q и количества образцов s
для i = 1,…, s do
образца и
вычислить с использованием уравнения 21
если ρ < u то
комплект
образец λ ( i ) ∼ p (⋅ | μ ( i ) , η ( i −1) , D ) с использованием уравнения 22
остальное
комплект
конец, если
для j = 1,…, N do
с использованием алгоритма 2 с μ = μ ( i ) , z = z ( i −1) , λ = λ ( i )
конец для
для j = 1,…, N do
с использованием уравнения 18
конец для
образец ω ( i ) ∼ p (⋅ | z ( i ) , D ) с использованием уравнения 17
конец для
возврат образца
Апостериорное распределение для будущих данных
Учитывая новую (будущую) точку данных ( d *, t *) от нового пациента, мы хотели бы вычислить вероятность того, имеет ли этот случай тот же самый штамм.Это можно вычислить из апостериорной части модели, подогнанной к данным D , D 0 следующим образом. Обозначим исходный вектор параметров с θ , как и раньше, и дополнительные параметры, связанные с новой точкой данных D * = {( d *, t *)} как z * ∈ {(1 , 0), (0, 1)} и. Обновленные апостериорные данные после рассмотрения новой точки данных D * затем (27) (28) (29) где p ( θ | D , D 0 ) — апостериор на основе наших исходных данных D , D 0 .Мы маргинализируем набор параметров, наименее способствующих достижению цели получения (30) (31) где для i = 1,…, s . Вероятность того, что новая точка измерения ( d *, t *) будет принадлежать к той же деформации, на основе ранее наблюдаемых данных D , D 0 получается из уравнения 31.
Результаты
В этом разделе мы подгоняем модель W-F к внешним данным D 0 , как описано в разделе ABC, чтобы обновить предыдущие с использованием внешних данных.Затем мы проверяем, что предложенный алгоритм выборки Гиббса для подбора модели смеси на основе байесовского вывода раздела для модели смеси согласован на основе экспериментов с смоделированными данными. Затем мы подгоняем модель смеси к данным MRSA и обсуждаем результаты. Наконец, мы оцениваем качество соответствия модели.
Обновление предыдущего с помощью вывода ABC
Апостериор ABC, основанный на внешних данных D 0 и несоответствии в уравнении 8, показан на рис. 5A.Мы также повторили вычисления, чтобы исключить из анализа подмножество пациентов A-M, то есть второй член суммирования в уравнении 8 был установлен на ноль. Это было сделано для оценки эффекта пациентов A-M, у которых есть измерения только с одной временной точки и неизвестное время с момента приобретения. Этот дополнительный анализ привел к апостериорной аппроксимации ABC, показанной на рис. 5B. Мы видим, что в обоих случаях большие части пространства параметров были исключены как имеющие пренебрежимо малую апостериорную вероятность. Как и ожидалось, апостериорное распределение на основе подмножества (рис. 5B) немного более рассредоточено, чем с полными данными D 0 (рис. 5A).Использование полных данных приводит к тому, что предполагаемая частота мутаций немного выше, чем с подмножеством, вероятно, потому, что модель должна учитывать более высокую вариабельность у пациентов A-M. Кроме того, малые эффективные размеры выборки ( n eff <2000) менее вероятны на основе полных данных D 0 .
Рис. 5. Апостериорное распределение ABC для ( n eff , μ ).
Апостериорное распределение ABC i.е. обновленные априорные параметры ( n eff , μ ), эффективный размер популяции и частота мутаций с учетом данных D 0 . Панель A показывает результат с полными данными, а панель B — соответствующий результат только с подмножеством данных (подробности см. В тексте).
https://doi.org/10.1371/journal.pcbi.1006534.g005
В целом мы видим, что эффективный размер выборки n eff нельзя точно определить на основе внешних данных D 0 только .Мы также видим, что если бы верхняя граница априорной плотности n eff была увеличена с 10 000, более высокие значения, вероятно, также имели бы немалую апостериорную вероятность; однако это ограничение будет иметь незначительное влияние на результирующую апостериорную модель смеси, как будет показано ниже. С другой стороны, частота мутаций μ с высокой вероятностью меньше 0,001 мутации на геном на поколение и не может быть сколь угодно малой.
Проверка модели смеси с использованием смоделированных данных
Для эмпирического исследования идентифицируемости параметров модели смеси, а также правильности и согласованности нашего алгоритма MCMC в предположении, что модель задана правильно, мы сначала подгоняем модель смеси к смоделированным данным.Мы генерируем искусственные данные из модели смеси со значениями параметров, аналогичными оценкам для наблюдаемых данных D из следующего раздела. В частности, мы выбираем n eff = 2, 137, μ = 0,0011, ω S = 0,8, λ = 0,0001 и повторяем анализ с различными размерами данных N . В остальном мы используем априорные значения, аналогичные реальным данным в следующем разделе, за исключением того, что для простоты вместо использования априорных значений, полученных из вывода ABC, мы используем унифицированные априорные значения в уравнении 7.Затем мы подгоняем модель смеси к смоделированным наборам данных, чтобы исследовать, можно ли восстановить истинные параметры (идентифицируемость) и концентрируются ли апостериорные значения вокруг своих истинных значений при увеличении объема данных (согласованность).
Результаты показаны на рис. 6. Мы видим, что (маргинальное) апостериорное значение ( n eff , μ ) сосредоточено вокруг истинного значения параметра, которое использовалось для генерации данных (зеленый ромб на рисунке) .Кроме того, несмотря на то, что количество параметров увеличивается в зависимости от размера данных N (поскольку каждая точка данных ( d i , t i ) имеет свой собственный индикатор класса z i и время до самого последнего общего предка t 0 i параметр), маргинальное апостериорное распределение ( n eff , μ ) может быть идентифицировано и, по-видимому, сходятся к истинному значению при увеличении N .Мы не можем точно узнать каждый t 0 i , поскольку по существу только точка данных, которой соответствует параметр, предоставляет информацию о его значении. Однако точные оценки этих мешающих параметров не требуются для использования модели или получения полезных оценок других неизвестных параметров, как показано на рис. 6.
Рис. 6. Точность и согласованность с синтетическими данными.
На первых трех панелях показаны оценочные апостериорные распределения для параметров ( n eff , μ ) модели смеси с использованием смоделированных данных различных размеров N .Зеленый ромб показывает истинное значение, используемое для генерации смоделированных данных, а светло-серые точки обозначают местоположения точек сетки, необходимые для численных расчетов. Нижняя правая панель показывает расчетный и истинный параметр ω S в наборе дополнительных экспериментов по моделированию.
https://doi.org/10.1371/journal.pcbi.1006534.g006
На панели в правом нижнем углу рис. 6 показаны результаты дополнительного имитационного эксперимента, в котором модель смеси соответствует данным, полученным с различными значениями для ω S параметр, который представляет долю пар, принадлежащих к одной и той же деформации.Помимо этого и того факта, что мы зафиксировали N = 150, экспериментальный план такой же, как и выше. Результаты показывают, что оценочные значения ω S в целом хорошо согласуются с истинными значениями. Интересно, что ω S немного переоценено, когда его истинное значение близко к 0, и немного занижено, когда истинное значение близко к 1, что может отражать регуляризирующий эффект априорного значения, отвлекая оценки от крайние значения.Кроме того, когда истинное значение ω S составляет около 0,5, дисперсия оценки имеет тенденцию быть выше, чем при значениях ω S , близких к 0 или 1. Это наблюдение можно объяснить. тем фактом, что существует больше точек данных, которые перекрывают обе компоненты модели смеси, когда ω S составляет около 0,5, что делает задачу вывода более сложной задачей и вызывает более высокую апостериорную дисперсию.
Анализ проекта ОЧИСТИТЬ данные MRSA
Следующие настройки используются для анализа продольной выборки S.aureus изоляты ноздрей из контрольной группы проекта CLEAR [24]. Мы генерируем 4 цепочки MCMC, каждая длиной 25 000, инициализируемых случайным образом из предыдущей плотности, чьи первые половины отбрасываются как «выгорание». Мы используем диагностику сходимости Гельмана и Рубина в коде R-пакета и визуальные проверки для оценки сходимости алгоритма MCMC. Мы используем эквидистантную сетку 100 × 100 для численных расчетов со значениями ( n eff , μ ) и s = 10 000 в уравнении 24.Апостериор ABC, полученный в разделе Обновление предыдущего с использованием вывода ABC. и визуализированный на фиг. 5A используется как априор для ( n eff , μ ).
Вектор параметров θ состоит из «глобальных» параметров n eff , μ , ω , λ, а также большого количества мешающих параметров ( z и t 0 ), относящиеся к каждой точке данных. Расчетные глобальные параметры представлены в таблице 1.Мы также повторили анализ, используя однородный предварительный анализ ( n eff , μ ). Хотя унифицированный априор не информативен относительно параметров ( n eff , μ ), результаты, тем не менее, на удивление похожи (таблица 1). Другими словами, дополнительные данные D 0 , используемые для обновления предшествующих, имеют лишь небольшое влияние на оценочные параметры модели смеси. Это было неожиданно, потому что набор данных D , используемый для обучения модели смеси, имеет только один геном на выбранный момент времени, и все же, что впечатляет, модель может узнать о параметрах ( n eff , μ ), которые эффективно определяют изменчивость во всей популяции.Это дополнительно демонстрирует устойчивость модели смеси к ранее использованной. Однако мы наблюдаем, что включение априорной точки из ABC немного сдвигает распределение вероятностей для n eff в сторону больших значений, хотя разница небольшая. Например, как показано в Таблице 1, 95% доверительный интервал (CI) для n eff , [1100, 1900] обновляется до [1100, 2000], когда добавляется дополнительная априорная информация.
На рис. 7 показано апостериорное прогнозирующее распределение для вероятности того же случая деформации для (гипотетического будущего) наблюдения с расстоянием d * и разницей во времени t *.Синий цвет на рисунке означает высокую вероятность того же штамма. Соответствующая 50% классификационная кривая представляет собой (почти) прямую линию с крутым положительным наклоном. Это ожидаемо, поскольку одна и та же модель штамма может объяснить большее количество мутаций по прошествии большего количества времени. Приблизительно 20 мутаций проводят грань между одним и тем же штаммом и случаями разных штаммов в пределах разницы во времени до 6000 поколений. Неопределенность в классификации возникает из-за перекрытия двух объяснений (около d * ≈ 20) и из-за апостериорной неопределенности в параметрах модели θ .
Рис. 7. Результаты проекта CLEAR MRSA data.
Контурная диаграмма для одинаковой вероятности деформации расстояния d * и временного интервала t * на основе подобранной модели. Цветные точки обозначают наблюдения, которые использовались для соответствия модели. Синий цвет указывает на большую вероятность одинаковой деформации. Расстояния больше 50 не показаны и с вероятностью единица классифицируются как разные деформации. 6000 поколений на оси ординат соответствуют приблизительно одному году.
https://doi.org/10.1371/journal.pcbi.1006534.g007
Мы также подробно проанализировали все наблюдаемые закономерности, где: 1) два генома одного и того же ST от одного и того же пациента чередуются с отсутствующим наблюдением, то есть колонизацией кажется, что исчезает, а затем снова появляется, и 2) два генома одного и того же ST от одного и того же пациента чередуются с наблюдением другого ST. Номера для двух геномов, принадлежащих к одному или разному штамму в этих паттернах, показаны в таблице 2.Достоверные интервалы для пропорции «одинаковой деформации» сочетают в себе неопределенность от ограниченного числа образцов с апостериорной неопределенностью того, принадлежит ли образец той же самой деформации или нет (более подробную информацию см. В дополнительном материале). Из таблицы 2 мы видим, что примерно 69% пар геномов в паттерне 1) принадлежат к одному и тому же штамму. Это лишь немного меньше той же пропорции деформации, если между ними нет пропущенных наблюдений (89%). Следовательно, правдоподобное объяснение большинства отсутствующих промежуточных наблюдений состоит в том, что на самом деле один и тот же штамм колонизировал пациента на всем протяжении, а отсутствующее наблюдение отражает ограниченную чувствительность выборки, а не клиренс с последующим новым приобретением.Точно так же, даже если они чередуются с другим ST (образец 2), окружающие геномы часто, в 65% случаев, по-видимому, принадлежат к одному и тому же штамму. Это говорит о том, что в этих случаях пациент был колонизирован окружающим штаммом повсюду и был совместно колонизирован двумя разными ST во время наблюдения за расходящимся ST посередине.
Таблица 2. Расчетное количество (среднее значение, 95% ДИ в скобках) случаев с геномами в начале и в конце образца, принадлежащими одному или разному штамму, для трех разных образцов в данных Project CLEAR MRSA, и расчетная доля случаев одинаковой деформации.
https://doi.org/10.1371/journal.pcbi.1006534.t002
Наконец, мы вычисляем коэффициенты захвата и очистки, используя нашу модель, и сравниваем их с теми, которые получены с помощью обычной стратегии использования порога фиксированного расстояния. Для целей этого описания мы неофициально определяем приобретение r acq и коэффициенты клиренса r clear как (32) где величины A , B , C , D и E обозначают количество возможных событий в последовательных выборках (например,грамм. получение, замена, удаление или отсутствие изменений), подробно определенное в таблице 3. Кроме того, G — это общее количество возможных событий по всем данным. Величины A , B , D и E являются случайными величинами, которые зависят от одинаковых / различных апостериорных вероятностей деформации, и, следовательно, мы также вычисляем оценки неопределенности для этих величин в уравнении 32. Число C равно константа, потому что наблюдаемое изменение ST также всегда указывает на фактическое изменение ST.Для случаев с одним или несколькими отрицательными образцами (обозначенными) между двумя положительными образцами мы не знаем, когда имели место события очистки и сбора и являются ли отрицательные образцы «ложноотрицательными». Чтобы справиться с этими случаями, мы экономно предполагаем, что отсутствующее наблюдение между двумя положительными образцами, которые предположительно происходят от одного и того же штамма, является ложноотрицательным (то есть тот же штамм присутствовал также в середине, даже если он не был обнаружен), и записать эти события в группы AE соответственно.Подробная информация о том, как мы однозначно определяем группу для всех особых случаев, представлена в Дополнительном материале.
Предполагаемые уровни приобретения и удаления с 95% вероятными интервалами показаны в последних двух строках таблицы 3. Для сравнения мы также вычислили эти показатели аналогичным образом, но с использованием фиксированного порога расстояния в 40 мутаций, значения, используемого в [10] , чтобы определить, принадлежат ли два генома к одному штамму или нет. Мы видим, что оценки, основанные на пороге, относительно похожи на оценки нашей модели и лишь немного меньше их.Объяснение подобия сводок, таких как частота получения и удаления, заключается в том, что при оценке этих величин по всему набору данных неопределенность усредняется, даже если некоторые отдельные точки данных демонстрируют большую неопределенность относительно того, являются ли они одинаковыми. деформации или нет (см. рис. 7). Важно отметить, что, несмотря на то, что наша модель соответствует предыдущим результатам, она обходит задачу эвристического выбора единственного порога и добавляет оценки неопределенности вокруг точечных оценок, что имеет решающее значение для получения строгих выводов.
Оценка соответствия модели для проекта CLEAR MRSA data
В качестве последней части нашего анализа мы используем апостериорные прогностические проверки для оценки качества модели, см., Например, [16] для получения дополнительных сведений. Вкратце, это состоит из моделирования реплицированных наборов данных D rep, ( j ) из подобранной модели смеси и сравнения их с наблюдаемыми данными D для любых систематических отклонений. Любые расхождения между наблюдаемыми и смоделированными данными можно использовать для критики модели и понимания того, как ее можно улучшить.На практике моделирование повторяющихся данных выполняется путем моделирования вектора параметров θ ( j ) от апостериорного (с использованием существующей цепочки MCMC) и моделирования нового набора пар разницы расстояния-времени в D rep, ( j ) из модели с использованием θ ( j ) . Чтобы получить реплик M , эта процедура повторяется для j = 1,…, M .
Примеры повторяющихся наборов данных показаны на рис. 8. В целом смоделированные расстояния аналогичны соответствующим наблюдениям. Чаще всего встречаются небольшие расстояния, и частота уменьшается с увеличением расстояния. Случайные большие расстояния ( d i > 20) встречаются очень редко, что согласуется с данными наблюдений. Небольшое несоответствие заключается в том, что подобранная модель имеет тенденцию недооценивать частоту нулевого расстояния, в то время как небольшие положительные расстояния имеют тенденцию встречаться чаще, чем наблюдаемые.Это могло произойти, потому что мы оценили эмпирические плотности p sim ( d i 1 | n eff , μ ), используя постоянное время 6000 (т.е. 1 год) с момента получения (как описано в разделе «Байесовский вывод для модели смеси»), что может привести к небольшому завышению оценок расстояний. Для дальнейшего изучения влияния этого предположения мы повторили анализ, чтобы вычислить плотности p sim ( d i 1 | n eff , μ ) при постоянной время 1 000 поколений.Однако несоответствие не исчезло полностью, и оценочная частота мутаций увеличилась в результате, чтобы компенсировать возникновение больших расстояний, в отличие от предшествующей плотности из анализа ABC и данных D 0 . Таким образом, мы считаем, что нынешняя модель является адекватной.
Рис. 8. Проверка модели с использованием апостериорной прогнозной проверки.
Гистограмма в верхнем левом углу показывает наблюдаемое распределение расстояний в данных Project CLEAR MRSA, другие цифры в двух верхних строках показывают соответствующие расстояния в повторяющихся наборах данных, смоделированных на основе подобранной модели.В двух нижних строках показаны те же гистограммы, увеличенные до диапазона [0, 50]. Наборы реплицируемых данных в целом выглядят аналогично наблюдаемым данным, что демонстрирует адекватность модели. Однако количество нулевых расстояний недооценивается, а частоты малых положительных расстояний имеют тенденцию слегка завышаться.
https://doi.org/10.1371/journal.pcbi.1006534.g008
Обсуждение
Мы представили новую модель для анализа клиренса и приобретения бактериальной колонизации, которая, в отличие от предыдущих подходов, не полагается на эвристический фиксированный порог расстояния, чтобы определить, принадлежат ли геномы, наблюдаемые в разные моменты времени, к одинаковым или разным. получение.Полностью вероятностная модель автоматически предоставляет оценки неопределенности для всех соответствующих величин. Кроме того, он учитывает изменение временных интервалов между парами последовательных выборок. Еще одно преимущество заключается в том, что модель может легко включать дополнительные внешние данные для информирования о значениях параметров. Чтобы соответствовать модели, мы разработали инновационную комбинацию ABC и MCMC, основанную на базовой модели смеси, в которой одно из распределений компонентов было сформулировано эмпирически путем моделирования.
Мы продемонстрировали модель, используя данные о геномах S. aureus , взятых продольно у нескольких пациентов. Наш анализ предоставил доказательства случайной совместной колонизации и выявил вероятные ложноотрицательные образцы. Результат модели состоит из одной и той же вероятности штамма в сравнении с разной вероятностью штамма для любой пары геномов, и, используя эту информацию для решения (вероятностно), когда и где колонизирующий штамм изменился, можно было легко рассчитать скорости приобретения и клиренса.Было обнаружено, что оценки этих параметров согласуются с предыдущими оценками, полученными с использованием фиксированного порога, но теперь мы смогли предоставить доверительные интервалы, необходимые для получения строго обоснованных выводов. Мы считаем, что такой анализ достаточно распространен, поэтому наш метод должен быть полезен для многих, и, следовательно, мы предоставляем его как простой в использовании R-код. Код включает инструменты как для ABC-вывода, чтобы включить внешние данные о распределении расстояний между несколькими выборками в заданный момент времени (или два момента времени), так и алгоритм MCMC.Отметим, что наш метод не предполагает рекомбинации. Поэтому мы рекомендуем удалять рекомбинации, предварительно обработав геномы одним из стандартных методов [35–37], как мы это делали в нашем анализе. Хотя наш анализ продемонстрировал, что внешние данные могут уменьшить неопределенность конечных апостериорных данных, мы также увидели, что метод может работать без таких данных. В последнем случае входные данные представляют собой просто список пар разницы между расстоянием и временем для геномов, взятых у одного и того же пациента в последовательные моменты времени, и достаточно запустить MCMC, который в типичных случаях является эффективным и быстрым.
Центральным компонентом нашего подхода является модель вариации внутри хозяина, необходимая для определения того, сколько вариаций можно ожидать, если геномы в разные моменты времени произошли от одного и того же штамма, полученного за одно приобретение. Для этой цели мы выбрали базовую модель Райта-Фишера, предполагающую постоянный размер популяции и частоту мутаций, с пониманием того, что эти предположения, как ожидается, будут в некоторой степени нарушены в любом реалистичном наборе данных, но преимущества простоты включают надежность выводов, сделанных ранее. распределения и идентифицируемость параметров по имеющимся данным.Более сложные модели были приспособлены к распределению расстояний (наши внешние данные D 0 ), предполагая, что размер популяции сначала увеличивается, а затем уменьшается [14]. Однако наша модель может соответствовать тем же данным с меньшим количеством параметров, что оправдывает более простую альтернативу. Кроме того, постоянный размер популяции также можно рассматривать как разумную модель постоянной колонизации. Интересный вопрос будущих исследований — какие дополнительные данные следует собрать, чтобы соответствовать одному из возможных расширений базовой модели.
Недавно были разработаны другие методы с целью определения случаев передачи инфекции между родственными пациентами [38]. Однако цель нашего метода иная: изучить динамику приобретения и исчезновения колонизации с использованием данных независимых пациентов. Тем не менее, потенциальное расширение нашей модели, которое могло бы позволить изучать передачу между близкородственными людьми, например, внутри домохозяйства, могло бы включать несколько взаимосвязанных популяций, по одной для каждого возможного хозяина, аналогично тому, что рассматривается здесь для одного хозяина.Еще одно направление, которое мы в настоящее время преследуем, — это расширить модель, чтобы охватить геномы, взятые из нескольких участков тела.
% PDF-1.4 % 23 0 объект > / OCGs [26 0 R] >> / Страницы 19 0 R / Тип / Каталог >> эндобдж 25 0 объект > / Шрифт >>> / Поля [] >> эндобдж 20 0 объект > поток 2021-06-21T15: 56: 51-07: 002005-09-10T18: 07: 39 + 05: 302021-06-21T15: 56: 51-07: 00uuid: 2b0426bc-589b-49d8-9f97-c24314fc9af1uuid: 2296001a- 1dd2-11b2-0a00-b8001886cdffapplication / pdf конечный поток эндобдж 19 0 объект > эндобдж 27 0 объект > / Font> / T1_1> / T1_2> / T1_3> / T1_4 43 0 R >> / ProcSet [/ PDF / Text / ImageB] / Properties> / XObject >>> / Rotate 0 / Type / Page >> эндобдж 1 0 объект > / Font> / T1_1> / T1_2> / T1_3> / T1_4> / T1_5> / T1_6> / T1_7 43 0 R >> / ProcSet [/ PDF / Text / ImageB] / Properties> / XObject >>> / Rotate 0 / Тип / Страница >> эндобдж 6 0 obj > / Font> / T1_1> / T1_2> / T1_3> / T1_4> / T1_5> / T1_6> / T1_7> / T1_8> / T1_9 43 0 R >> / ProcSet [/ PDF / Text / ImageB] / Свойства> / XObject >>> / Повернуть 0 / Тип / Страница >> эндобдж 11 0 объект > / Font> / T1_1> / T1_2> / T1_3> / T1_4> / T1_5> / T1_6 43 0 R >> / ProcSet [/ PDF / Text / ImageB] / Properties> / XObject >>> / Rotate 0 / Type / Страница >> эндобдж 40 0 объект > / ProcSet [/ PDF / Text / ImageC] / XObject >>> / Type / Page >> эндобдж 50 0 объект [56 0 R 57 0 R 58 0 R 59 0 R 60 0 R] эндобдж 51 0 объект > поток q 539.3594055 0 0 83.3014526 36.3202972 660.6985474 см / Im0 Do Q BT / T1_0 1 Тс 10 0 0 10 105,56995 562,99985 тм (1997; 3: 1535-1538.) Tj / T1_1 1 Тс -7.55699 0 Тд (Clin Cancer Res \ 240) Tj / T1_0 1 Тс 0 1 ТД (\ 240) Tj 0 1.00001 TD (П. Бай, Р. Бруно, Дж. Х. Шелленс и др.) Т. Дж. / T1_2 1 Тс 0 1 ТД (\ 240) Tj / T1_3 1 Тс 18 0 0 18 30 602,99997 тм (доцетаксел \ (Таксотер \) очистка.) Tj Т * (Оптимальные стратегии выборки для байесовской оценки) Tj ET 30 508 552 35 рэ 0 0 мес. S BT / T1_0 1 Тс 11 0 0 11 120.94202 515.99997 тм (\ 240) Tj / T1_3 1 Тс -7.55696 1 тд (Обновленная версия) Tj ET BT / T1_2 1 Тс 10 0 0 10 141 507,99994 тм (\ 240) Tj / T1_0 1 Тс 23,56695 1 тд () Tj 0 0 1 рг -23.56695 0 Тд (http://clincancerres.aacrjournals.org/content/3/9/1535)Tj 0 г 0 1.00001 TD (См. Самую последнюю версию этой статьи по адресу:) Tj ET BT / T1_2 1 Тс 10 0 0 10 30 487,99997 тм (\ 240) Tj 0 1 ТД (\ 240) Tj ET BT / T1_2 1 Тс 10 0 0 10 30 467,99997 тм (\ 240) Tj Т * (\ 240) Tj ET BT / T1_2 1 Тс 10 0 0 10 30 447,99997 тм (\ 240) Tj Т * (\ 240) Tj ET 30 333 552 115 рэ 0 0 мес. S BT / T1_0 1 Тс 11 0 0 11 120.94202 415,99997 тм (\ 240) Tj / T1_3 1 Тс -5.66901 1 тд (Оповещения по электронной почте) Tj ET BT / T1_0 1 Тс 10 0 0 10 295,4996 428 тм (относится к этой статье или журналу.) Tj 0 0 1 рг -15.44996 0 Тд (Зарегистрируйтесь, чтобы получать бесплатные уведомления по электронной почте) Tj ET BT 0 г / T1_0 1 Тс 11 0 0 11 120.94202 382.99994 тм (\ 240) Tj / T1_3 1 Тс -6.38997 1 тд (Подписки) Tj 0,556 1,00001 тд (Отпечатки и) Tj ET BT / T1_0 1 Тс 10 0 0 10 141 385,99994 тм (\ 240) Tj 13,46496 1 тд (.) Tj 0 0 1 рг -6.85098 0 Тд ([email protected]) Tj 0 г -6.61398 0 Тд (Отделение) Tj 0 1.00001 TD (Чтобы заказать перепечатку статьи или подписаться на журнал, свяжитесь с нами \ t Публикации AACR) Tj ET BT / T1_0 1 Тс 11 0 0 11 120.94202 360.99997 тм (\ 240) Tj / T1_3 1 Тс -5.66901 1 тд (Разрешения) Tj ET BT / T1_0 1 Тс 10 0 0 10 141 332,99988 тм (\ 240) Tj 0 1 ТД (Сайт Rightlink.) Tj 0 1.00001 TD (Нажмите «Запросить разрешения», чтобы перейти на страницу защиты авторских прав \ Центр раннса \ (CCC \)) Tj 23,56695 1 тд (.

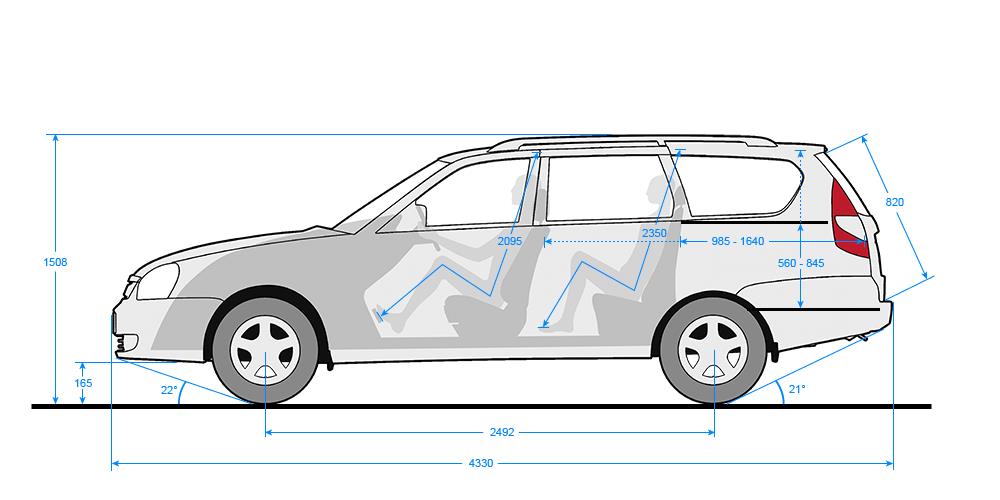
 Развивая тему безопасности, следует вспомнить о целесообразности покупки пластиковых проставок как более надежных.
Развивая тему безопасности, следует вспомнить о целесообразности покупки пластиковых проставок как более надежных.
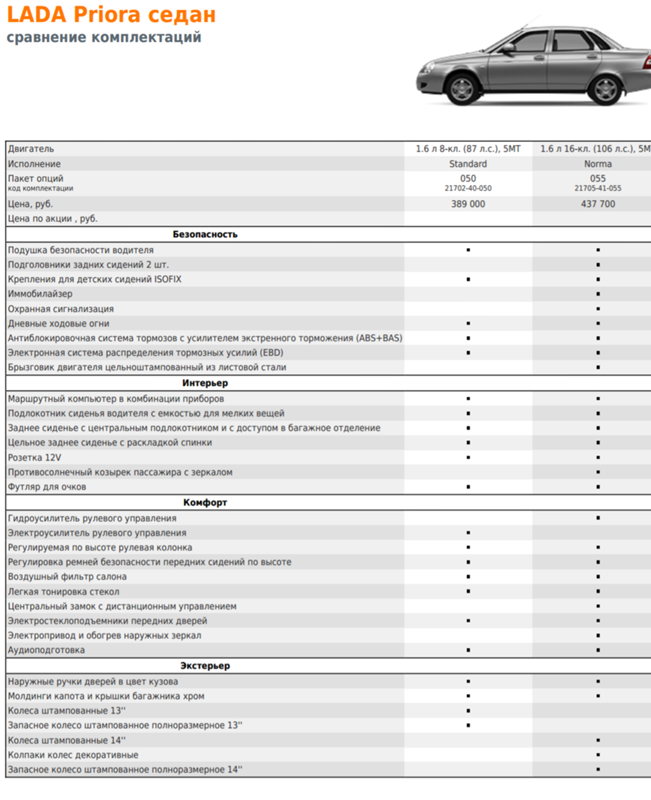
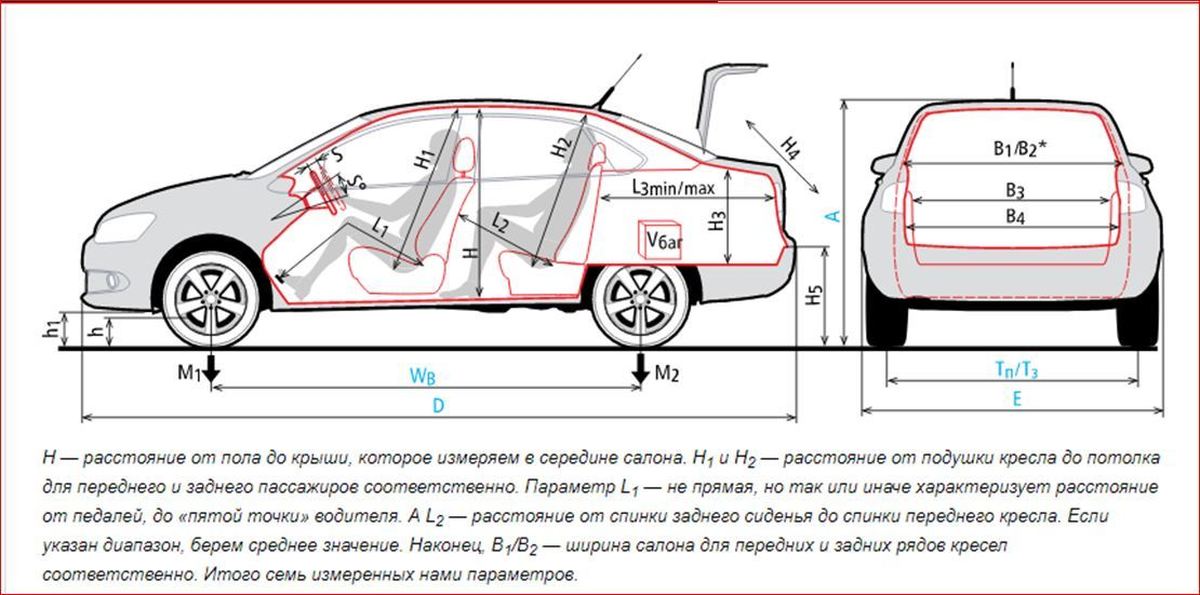 В целом машина меня устраивает. Днищем не чиркает. Ездил пока только на дачу- клиренс нормальный.
В целом машина меня устраивает. Днищем не чиркает. Ездил пока только на дачу- клиренс нормальный.

 В качестве альтернативы можно использовать медианную ковариату нового набора данных, но THETAP должен быть соответствующим образом скорректирован, и важно учитывать, что неопределенность параметра, которая зависит от нормализации, может быть смещена.
В качестве альтернативы можно использовать медианную ковариату нового набора данных, но THETAP должен быть соответствующим образом скорректирован, и важно учитывать, что неопределенность параметра, которая зависит от нормализации, может быть смещена. Ст.
Ст.