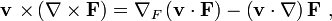Ротор что такое: Значение слова РОТОР. Что такое РОТОР? – Ротор (футбольный клуб) — Википедия
Значение слова РОТОР. Что такое РОТОР?
Ро́тор — (от лат. roto — вращаться)В математике:
Ротор — то же, что вихрь векторного поля, то есть вектор, характеризующий вращательное движение в данной точке векторного поля.
Ротор многогранника — выпуклое тело способное свободно вращаться в многограннике постоянно касаясь всех его граней; см. тело постоянной ширины и фигура постоянной ширины.
В медицине:
Синдром Ротора — одна из четырёх форм синдрома гипербилирубинемии.
В технике:
Ротор — вращающаяся часть двигателей и рабочих машин, на которой расположены органы, получающие энергию от рабочего тела (например, ротор двигателя Ванкеля) или отдающие её рабочему телу (например, ротор роторного насоса). Ротор двигателей связан с ведущим валом, ротор рабочих машин — с приводным валом. Ротор выполняется в виде барабанов, дисков, колёс.
Ротор — вращающаяся часть паровой турбины, компрессора, гидронасоса, гидромотора и т. д.
Буровой ротор — механизм, являющийся многофункциональным оборудованием буровой установки, который предназначен для вращения бурильных труб и поддержания колонны бурильных или обсадных труб при свинчивании и развинчивании в процессе спуско-подъемных операций, при поисковом бурении и капитальном ремонте скважин. Привод — цепной или карданный. Роторное бурение.
Ротор — устройство управления поворотом антенны в направлении приёма или передачи сигнала.
Ротор — любое вращающееся тело в теории балансировки.
Ротор — система вентилятора.
В электротехнике:
Ротор — вращающаяся часть электрической машины (генератора или двигателя переменного тока внутри неподвижной части — статора). Ротор асинхронной электромашины обычно представляет собой собранное из листовой электротехнической стали цилиндрическое тело с пазами для размещения обмотки. Ротор в электромашинах постоянного тока называется якорем.
Ротор — автоматически управляемая машина (транспортное устройство, прибор), в которой заготовки двигаются вместе с обрабатывающими их орудиями по дугам окружности. Роторная печь. Роторный экскаватор. Роторная линия (комплекс роторов).
В авиации:
Ротор — несущий винт вертолёта.
В ветроэнергетике:
Ротор Дарье — составная часть вертикально-осевого ветрогенератора, крыльчатка которого представляет собой двояковыпуклые лопасти, закреплённые при помощи штанг на вертикально вращающейся оси.
Ротор Савониуса — составная часть вертикально-осевого ветрогенератора в виде двух смещенных относительно друг друга полуцилиндрических лопастей и небольшого (10—15 % от диаметра лопасти) перекрытия, которые образуют параллельно оси вращения ротора.
В судостроении:
Ротор Флеттнера — «парусная мачта» или заменяющий паруса ротор (на судне их устанавливается несколько), с помощью которого судно приводится в движение посредством ветра, благодаря эффекту Магнуса. Роторное судно Флеттнера.
Собственные имена:
Ротор, Артуро (1907—1988) — филиппинский врач, государственный служащий, музыкант и писатель.
РОТОР — Сетевой конкурс «Российский Онлайн ТОР».
НПО «Ротор» — предприятие — разработчик и производитель гироскопических приборов для ракетно-космической техники (СССР, Россия).
Приборостроительный завод «Ротор» — промышленное предприятие в Барнауле.
«Ротор» — футбольный клуб из Волгограда.
«Ротор-Волгоград» — пляжный футбольный клуб из Волгограда.
«Ротор» — тренировочная база в Волгограде.
«Ротор» — официальный журнал волгоградского футбольного клуба.
РОТОР (Российский Онлайн ТОР; произносится «ро́тор») — сетевой конкурс, организованный Международным союзом интернет-деятелей «ЕЖЕ». Впервые был проведён в 1999 году.Целями являются выявление значимых проектов и персоналий Рунета и определение тенденций его развития.
Члены жюри РОТОРа, подписчики дискуссионного мейл-листа «ЕЖЕ», сами являются значимыми и опытными интернет-деятелями, авторами различных сетевых проектов, что придаёт конкурсу авторитетность.
Ротор — это… Что такое Ротор?
Ротор-2 — Основан 2001 Соревнование второй дивизион ПФЛ, Зона Юг 2005 3 … Википедия
РОТОР — РОТОР, центральная часть электрического ДВИГАТЕЛЯ или ГЕНЕРАТОРА. В большинстве устройств ротор состоит из нескольких проволочных катушек, надетых на стержень, который вращается в магнитном поле. В электродвигателе ротор вращается, когда сквозь… … Научно-технический энциклопедический словарь
ротор — вихрь Словарь русских синонимов. ротор сущ., кол во синонимов: 4 • гидроротор (1) • … Словарь синонимов
РОТОР — то же, что вихрь векторного поля … Большой Энциклопедический словарь
РОТОР — (от лат. roto вращаюсь) вращающаяся деталь машин, обычно расположенная внутри статора, напр. в электродвигателях, турбинах … Большой Энциклопедический словарь
РОТОР — РОТОР, ротора, муж. (от лат. roto вращаю) (тех.). 1. Вращающаяся часть в электромашинах и турбинах, в противоп. статору. 2. Устройство на судах в виде вертикально поставленных труб, служащее для приведения в движение судна силой ветра (мор.).… … Толковый словарь Ушакова
РОТОР — РОТОР, а, муж. (спец.). 1. Вращающаяся часть в машинах. 2. Автоматически управляемая машина (транспортное устройство, прибор), в к рой заготовки двигаются вместе с обрабатывающими их орудиями по дугам окружности. | прил. роторный, ая, ое.… … Толковый словарь Ожегова
РОТОР — (от лат. roto вращаю) (вихрь) одна из осн. операций векторногоанализа, сопоставляющая векторному полю а(r )др. векторное полеrot а (используются также обозначения curl а). Если точка r задана своими декартовыми координатами, а вектор а своими… … Физическая энциклопедия
РОТОР — (Rotor) вращающаяся часть двигателей и машин вращательного типа в виде барабанов, дисков и колес, снабженных устройством для преобразования энергии рабочего вещества в механическую работу или работы в какой либо вид энергии. В электрических… … Морской словарь
РОТОР — вращающаяся часть электр. машин. Термин этот применяется гл. обр. к машинам переменного тока (генераторам и моторам). Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н.… … Технический железнодорожный словарь
ротор — якорь. EdwART. Словарь автомобильного жаргона, 2009 … Автомобильный словарь
РОТОР++ — это… Что такое РОТОР++?

Размещение текста, ранее находившегося на этой странице, возможно, нарушает авторские права. Ранее удалённый текст был опубликован в следующем источнике:
- http://ezhe.ru/POTOP/about.html
Если вы хотите переписать статью, делайте это здесь: РОТОР/Temp.
Эта страница внесена в категорию «Википедия:Возможное нарушение авторских прав».
В обсуждение участнику, создавшему эту статью, следует выставить сообщение {{subst:nothanks cv|РОТОР|url=http://ezhe.ru/POTOP/about.html}} —~~~~
Вниманию участника, разместившего эту статью
Не редактируйте её сейчас, даже если вы собираетесь её переписать (следуйте указаниям ниже).
Если владелец авторских прав на указанный выше материал разрешает использовать его на условиях GNU FDL, или если правообладателем являетесь вы, пожалуйста, действуйте согласно описанию на странице ВП:ДОБРО.
Если же разрешения на использование этого материала нет, то просим вас:
- либо написать хотя бы хорошую болванку статьи на этой подстранице,
- либо оставить всё как есть, и тогда статья будет удалена.
Не следует копировать нарушающий авторские права текст на указанную подстраницу и редактировать его. Если факт нарушения авторских прав подтвердится, статья будет удалена вместе с подстраницей. Если вы взялись за написание новой статьи, не забудьте сообщить об этом на странице обсуждения.
В случае если новый текст написан не будет, эта статья будет удалена через одну неделю после появления настоящего предупреждения.
Исходный (возможно, нарушающий авторские права) текст этой статьи можно найти в истории изменений.
Обратите внимание, что размещение в Википедии материалов, автор которых не дал явного разрешения на их использование в соответствии с лицензией GNU FDL, может являться нарушением законов об авторском праве. К участникам Википедии, систематически допускающим размещающие таких текстов, могут быть применены меры по техническому ограничению возможности редактировать страницы проекта.
Несмотря ни на что, мы всегда рады вашим оригинальным статьям.
Спасибо.
Если вы автор этой статьи, прочтите руководство к дальнейшему действию
РОТОР — это… Что такое РОТОР?
Ротор-2 — Основан 2001 Соревнование второй дивизион ПФЛ, Зона Юг 2005 3 … Википедия
ротор — вихрь Словарь русских синонимов. ротор сущ., кол во синонимов: 4 • гидроротор (1) • … Словарь синонимов
РОТОР — то же, что вихрь векторного поля … Большой Энциклопедический словарь
РОТОР — (от лат. roto вращаюсь) вращающаяся деталь машин, обычно расположенная внутри статора, напр. в электродвигателях, турбинах … Большой Энциклопедический словарь
РОТОР — РОТОР, ротора, муж. (от лат. roto вращаю) (тех.). 1. Вращающаяся часть в электромашинах и турбинах, в противоп. статору. 2. Устройство на судах в виде вертикально поставленных труб, служащее для приведения в движение судна силой ветра (мор.).… … Толковый словарь Ушакова
РОТОР — РОТОР, а, муж. (спец.). 1. Вращающаяся часть в машинах. 2. Автоматически управляемая машина (транспортное устройство, прибор), в к рой заготовки двигаются вместе с обрабатывающими их орудиями по дугам окружности. | прил. роторный, ая, ое.… … Толковый словарь Ожегова
РОТОР — (от лат. roto вращаю) (вихрь) одна из осн. операций векторногоанализа, сопоставляющая векторному полю а(r )др. векторное полеrot а (используются также обозначения curl а). Если точка r задана своими декартовыми координатами, а вектор а своими… … Физическая энциклопедия
РОТОР — (Rotor) вращающаяся часть двигателей и машин вращательного типа в виде барабанов, дисков и колес, снабженных устройством для преобразования энергии рабочего вещества в механическую работу или работы в какой либо вид энергии. В электрических… … Морской словарь
РОТОР — вращающаяся часть электр. машин. Термин этот применяется гл. обр. к машинам переменного тока (генераторам и моторам). Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н.… … Технический железнодорожный словарь
ротор — якорь. EdwART. Словарь автомобильного жаргона, 2009 … Автомобильный словарь
Ротор — Википедия. Что такое Ротор
Материал из Википедии — свободной энциклопедии Роторный экскаватор как экспонат в бывшем угольном карьере — «стальном городе» Феррополис (Германия), превращенном в музей под открытым небом
Роторный экскаватор как экспонат в бывшем угольном карьере — «стальном городе» Феррополис (Германия), превращенном в музей под открытым небомРо́тор (от лат. roto «вращаться»):
- в математике
- Ротор — то же, что вихрь векторного поля, то есть вектор, характеризующий вращательное движение в данной точке векторного поля.
- Ротор многогранника — выпуклое тело способное свободно вращаться в многограннике постоянно касаясь всех его граней; см. тело постоянной ширины и фигура постоянной ширины.
- в медицине
- в технике
- Ротор — вращающаяся часть двигателей и рабочих машин, на которой расположены органы, получающие энергию от рабочего тела (например, ротор двигателя Ванкеля) или отдающие её рабочему телу (например, ротор роторного насоса). Ротор двигателей связан с ведущим валом, ротор рабочих машин — с приводным валом. Ротор выполняется в виде барабанов, дисков, колёс.
- Ротор — вращающаяся часть паровой турбины, компрессора, гидронасоса, гидромотора и т. д.
- Буровой ротор — механизм, являющийся многофункциональным оборудованием буровой установки, который предназначен для вращения бурильных труб и поддержания колонны бурильных или обсадных труб при свинчивании и развинчивании в процессе спуско-подъемных операций, при поисковом бурении и капитальном ремонте скважин. Привод — цепной или карданный. Роторное бурение.
- Ротор — устройство управления поворотом антенны в направлении приёма или передачи сигнала.
- Ротор — любое вращающееся тело в теории балансировки.
- Ротор — система вентилятора.
- в электротехнике
- Ротор — вращающаяся часть электрической машины (генератора или двигателя переменного тока внутри неподвижной части — статора). Ротор асинхронной электромашины обычно представляет собой собранное из листовой электротехнической стали цилиндрическое тело с пазами для размещения обмотки. Ротор в электромашинах постоянного тока называется якорем.
- Ротор — автоматически управляемая машина (транспортное устройство, прибор), в которой заготовки двигаются вместе с обрабатывающими их орудиями по дугам окружности. Роторная печь. Роторный экскаватор. Роторная линия (комплекс роторов).
- в авиации
- в ветроэнергетике
- Ротор Дарье — составная часть вертикально-осевого ветрогенератора, крыльчатка которого представляет собой двояковыпуклые лопасти, закреплённые при помощи штанг на вертикально вращающейся оси.
- Ротор Савониуса — составная часть вертикально-осевого ветрогенератора в виде двух смещенных относительно друг друга полуцилиндрических лопастей и небольшого (10—15 % от диаметра лопасти) перекрытия, которые образуют параллельно оси вращения ротора.
- в судостроении
- Ротор Флеттнера — «парусная мачта» или заменяющий паруса ротор (на судне их устанавливается несколько), с помощью которого судно приводится в движение посредством ветра, благодаря эффекту Магнуса. Роторное судно Флеттнера.
- собственные имена
- Ротор, Артуро (1907—1988) — филиппинский врач, государственный служащий, музыкант и писатель.
- РОТОР — Сетевой конкурс «Российский Онлайн ТОР».
- НПО «Ротор» — предприятие — разработчик и производитель гироскопических приборов для ракетно-космической техники (СССР, Россия).
- Приборостроительный завод «Ротор» — промышленное предприятие в Барнауле.
- «Ротор» — футбольный клуб из Волгограда (в 2015—2018 годах «Ротор-Волгоград»).
- «Ротор-2» — фарм-клуб футбольного клуба «Ротор».
- «Ротор-2» — название футбольного клуба «Динамо» Михайловка в 1997 году.
- «Ротор-Волгоград» — пляжный футбольный клуб из Волгограда.
- «Ротор» — тренировочная база в Волгограде.
- «Ротор» — официальный журнал волгоградского футбольного клуба.
Ротор — футбольный клуб: новости клуба, состав команды, календарь и расписание матчей, статистика, видео
- Главная
- Футбол
- Матчи
- Новости
- Блоги
- Статусы
- Трансферы
- Россия
- Лига чемпионов
- Лига Европы
- Англия
- Испания
- Италия
- Германия
- Франция
- Сборные
- Олимп-ФНЛ
- Евро-2020
- Ливерпуль
- Тоттенхэм
- Челси
- Арсенал
- Зенит
- Барселона
- Реал Мадрид
- Спартак
- Сборная России
- Манчестер Юнайтед
- Салах
- Сон Хын Мин
- Азар
- Месси
- Роналду
- Головин
- Мбаппе
- Суарес
- Дзюба
- Неймар
- Хоккей
- Матчи
- Новости
- Блоги
- Статусы
- КХЛ
- НХЛ
- Кубок Первого канала
- Кубок Шпенглера
- Молодёжный чемпионат мира
- Шведские игры
- Чешские игры
- Юниорский чемпионат мира
- Зимняя классика НХЛ
- ФОНБЕТ Матч звезд КХЛ 2020
- Вашингтон
- СКА
- ЦСКА
- Авангард
- Тампа-Бэй
- Питтсбург
- Спартак
- Динамо Москва
- Рейнджерс
- Нью-Джерси
- Александр Овечкин
- Артемий Панарин
- Никита Кучеров
- Андрей Свечников
- Евгений Малкин
- Евгений Кузнецов
- Сергей Бобровский
- Андрей Василевский
- Никита Гусев
- Илья Михеев
- Баскетбол
- Матчи
- Новости
- Блоги
- Статусы
- НБА
- Turkish Airlines EuroLeague
- Единая лига ВТБ
- НБА плей-офф
- Зарплаты НБА
- Лейкерс
- ЦСКА
- Бостон
- Голден Стэйт
- Милуоки
- Торонто
- Чикаго
- Сан-Антонио
- Оклахома-Сити
- Зенит
- Сборная России
- Сборная США
- Леброн Джеймс
- Стефен Карри
- Кобе Брайант
- Джеймс Харден
- Кайри Ирвинг
- Кевин Дюрэнт
- Кавай Ленард
- Расселл Уэстбрук
- Алексей Швед
- Яннис Адетокумбо
- Авто
- Гонки
- Новости
- Блоги
- Статусы
- Формула 1
- MotoGP
- Формула 2
- Формула E
- Ралли Дакар
- Шелковый путь
- Феррари
- Макларен
- Ред Булл
- Мерседес
- Уильямс
- Хаас
- Торо Россо
- Рейсинг Пойнт
- Рено
- Альфа Ромео
- Льюис Хэмилтон
- Себастьян Феттель
- Роберт Кубица
- Даниил Квят
- Кими Райкконен
- Фернандо Алонсо
- Шарль Леклер
- Валттери Боттас
- Даниэль Риккардо
- Макс Ферстаппен
- Теннис
- Новости
- Блоги
- Статусы
- US Open
- Australian Open
- Ролан Гаррос
- Уимблдон
- Мужчины
- Женщины
- Кубок Дэвиса
- Новак Джокович
- Роджер Федерер
- Рафаэль Надаль
- Наоми Осака
- Симона Халеп
- Мария Шарапова
- Серена Уильямс
- Карен Хачанов
- Даниил Медведев
- Александр Зверев
- Эшли Барти
- Бокс/MMA/UFC
- Новости
- Блоги
- Статусы
- UFC
- MMA
- Бокс
- UFC 246
- UFC 247
- Бой Федора Емельяненко
- Бой Конор Макгрегор — Дональд Серроне
- Бой Хабиб – Тони Фергюсон
- Хабиб Нурмагомедов
- Конор Макгрегор
- Федор Емельяненко
- Александр Усик
- Василий Ломаченко
- Энтони Джошуа
- Деонтей Уайлдер
- Сауль Альварес
- Джон Джонс
- Александр Емельяненко
- Ставки
- Фигурное катание
- Новости
- Блоги
- Статусы
- Гран-при
- Чемпионат Европы
- Чемпионат мира
- Чемпионат России по фигурному катанию
- Сборная России
- Сборная Японии
- Сборная США
- Сборная Канады
- Сборная Франции
- Алена Косторная
- Алина Загитова
- Евгения Медведева
- Александра Трусова
- Анна Щербакова
- Михаил Коляда
- Елизавета Туктамышева
- Этери Тутберидзе
- Татьяна Тарасова
- Биатлон
- Гонки
- Новости
- Блоги
- Статусы
- Кубок мира
- Кубок IBU
- Чемпионат мира-2020
- Ижевская винтовка
- Сборная России
- Сборная России жен
- Сборная Германии
- Сборная Германии жен
- Сборная Норвегии
- Сборная Норвегии жен
- Александр Логинов
- Мартен Фуркад
- Йоханнес Бо
- Доротея Вирер
- Дмитрий Губерниев
- Лиза Виттоцци
- Светлана Миронова
- Екатерина Юрлова
- Дмитрий Малышко
- Стиль
- Лыжи
- Легкая атлетика
- Волейбол
- Регби
- Олимпиада-2020
- Американский футбол
- Бадминтон
- Бейсбол
- Бильярд/снукер
- Борьба
- Бобслей/сани/скелетон
- Велоспорт
- Водные виды
- Гандбол
- Гимнастика
- Гольф
- Гребля
- Единоборства
- Керлинг
- Конный спорт
- Коньки/шорт-трек
- Мини-футбол
- Настольный теннис
- Парусный спорт
- Пляжный футбол
- Покер
- Современное пятиборье
- Стрельба
- Триатлон
- Тяжелая атлетика
- Фехтование
- Хоккей на траве
- Хоккей с мячом
- Шахматы
- Экстремальные виды
- Экзотические виды
- Промокоды
- Финансы
- Прочие
- Главная
- Футбол
- Хоккей
- Баскетбол
- Авто
- Теннис
- Бокс/MMA/UFC
- Ставки
- Фигурное катание
- Биатлон
- Стиль
- Лыжи
- Легкая атлетика
- Волейбол
- Регби
- Олимпиада-2020
- Американский футбол
- Бадминтон
- Бейсбол
- Бильярд/снукер
- Борьба
- Бобслей/сани/скелетон
- Велоспорт
- Водные виды
- Гандбол
- Гимнастика
- Гольф
- Гребля
- Единоборства
- Керлинг
- Конный спорт
- Коньки/шорт-трек
- Мини-футбол
- Настольный теннис
- Парусный спорт
- Пляжный футбол
- Покер
- Современное пятиборье
- Стрельба
- Триатлон
- Тяжелая атлетика
- Фехтование
- Хоккей на траве
- Хоккей с мячом
- Шахматы
- Экстремальные виды
- Экзотические виды
- Промокоды
- Финансы
- Матч-центр
- Футбол
- Хоккей
- Баскетбол
- Авто
- Биатлон
- Новости
- Футбол
- Хоккей
- Баскетбол
- Теннис
- Авто
- Бокс/MMA/UFC
- Биатлон
- Фигурное катание
- Прочие
- Блоги
- Блоги
- Форумы
- Статусы
- Комментарии
- Футбол
- Россия
- Сборные
- Лига чемпионов
- Лига Европы
- Англия
- Испания
- Италия
- Германия
- Франция
- Украина
- Южная Америка
- Голландия
- Португалия
- Африка
- Любительский
- Азия
- Беларусь
- ФНЛ
- Хоккей
- 🏒Чемпионат мира по хоккею 2019
- Россия
- Сборные
- НХЛ
- КХЛ
- Баскетбол
- Turkish Airlines Euroleague
- Россия
- НБА
- Зарплаты НБА
- Еврокубки
- Сборные
- Еврочемпионаты
- Женский баскетбол
- Биатлон
- Чемпионат мира по биатлону
- Кубок мира по биатлону
- Теннис
- ATP
- WTA
- Кубок Дэвиса
- Кубок Федерации
- Ролан Гаррос
- Авто
- Формула-1
- Мото
- Ралли
- ДТМ
- Другие серии
- Бокс/MMA/UFC
- Бокс Профи
- ММА
- Прочее
- Фигурное катание
- Чемпионат мира по фигурному катанию
- Прочие
- Американский футбол
- Бадминтон
- Бейсбол
- Бильярд/снукер
- Борьба
- Бобслей/сани/скелетон
- Велоспорт
- Водные виды
- Волейбол
- Гандбол
- Гимнастика
- Гольф
- Гребля
- Единоборства
- Керлинг
- Конный спорт
- Коньки/шорт-трек
- Легкая атлетика
- Лыжи
- Мини-футбол
- Настольный теннис
- Парусный спорт
- Пляжный футбол
- Покер
- Регби
- Современное пятиборье
- Стрельба
- Триатлон
- Тяжелая атлетика
- Фехтование
- Хоккей на траве
- Хоккей с мячом
- Шахматы
- Экстрим
- Экзотические виды
- Трансферы
- Россия
- Англия
- Испания
- Италия
- Германия
- Франция
- Барселона
- Реал Мадрид
- Манчестер Юнайтед
- Ливерпуль
- Манчестер Сити
- Зенит
- Спартак
- ЦСКА
- Ювентус
- Подкасты
- Статусы
- Популярные
- Новые
- Рейтинг букмекеров
- Бонусы букмекеров
- Легальные
- Зарубежные
- Киберспортивные
- Мобильные
- Российские
- С кэшбеком
- Fantasy
- Fantasy
- Прогнозы
- Редакционные игры
- Киберспорт
- Прогнозы на спорт
Ротор (вектор) — это… Что такое Ротор (вектор)?
Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной литературе), а также 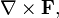 где
где  — векторный дифференциальный оператор набла.
— векторный дифференциальный оператор набла.
Математическое определение
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
 .
.
Нормаль 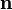 к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.
к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.
В трёхмерной декартовой системе координат 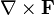 вычисляется следующим образом:
вычисляется следующим образом:
Для удобства запоминания можно условно представлять ротор как векторное произведение:
где i, j и k — единичные орты для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением
где 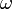 — вектор углового вращения элемента среды в точке О, а
— вектор углового вращения элемента среды в точке О, а 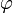 — квадратичная форма от координат — потенциал деформации элемента среды.
— квадратичная форма от координат — потенциал деформации элемента среды.
Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор 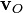 ), вращательного движения (вектор
), вращательного движения (вектор 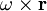 ) и потенциального движения — деформации (вектор
) и потенциального движения — деформации (вектор 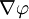 ). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство
). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство 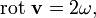 и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
Например, если в качестве векторного поля взять поле скоростей ветра на Земле, то в северном полушарии для антициклона, вращающегося по часовой стрелке, ротор будет направлен вниз, а для циклона, вращающегося против часовой стрелки — вверх. В тех местах, где ветры дуют прямолинейно и с одинаковой скоростью, ротор будет равен нулю (у неоднородного прямолинейного течения ротор ненулевой).
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
для любых векторных полей F и G и для всех вещественных чисел a и b.
- Если
 — скалярное поле, а F — векторное, тогда:
— скалярное поле, а F — векторное, тогда:
или
 или
или 
При этом верно и обратное: если поле F бездивергентно, оно есть поле вихря некоторого поля G:
- Если поле F потенциально, его ротор равен нулю (поле F — безвихревое):
Верно и обратное: если поле безвихревое, то оно потенциально:
для некоторого скалярного поля 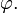
Ротор в ортогональных криволинейных координатах
![+ \frac{1}{H_3H_1}\left[\frac{\partial}{\partial q_3}(A_1H_1) - \frac{\partial}{\partial q_1}(A_3H_3)\right]\mathbf{q_2} + \frac{1}{H_1H_2}\left[\frac{\partial}{\partial q_1}(A_2H_2) - \frac{\partial}{\partial q_2}(A_1H_1)\right]\mathbf{q_3},](/800/600/https/dic.academic.ru/pictures/wiki/files/56/85425d94db549ba72b40f5c0e9152e66.png)
где Hi — коэффициенты Ламе.
Примеры
Простое векторное поле
![+ \frac{1}{H_3H_1}\left[\frac{\partial}{\partial q_3}(A_1H_1) - \frac{\partial}{\partial q_1}(A_3H_3)\right]\mathbf{q_2} + \frac{1}{H_1H_2}\left[\frac{\partial}{\partial q_1}(A_2H_2) - \frac{\partial}{\partial q_2}(A_1H_1)\right]\mathbf{q_3},](/800/600/https/dic.academic.ru/pictures/wiki/files/50/250px-uniform_curl.svg.png)
Рассмотрим векторное поле, линейно зависящее от координат x и y:
 .
.
Очевидно, что поле закручено. Если мы поместим колесо с лопастями в любой области поля, мы увидим, что оно начнет вращаться по направлению часовой стрелки. Используя правило правой руки, можно ожидать ввинчивание поля в страницу. Для правой системы координат направление в страницу будет означать отрицательное направление по оси z.
Вычислим ротор:
Как и предположили, направление совпало с отрицательным направлением оси z. В данном случае ротор является константой, так как он независим от координаты. Количество вращения в приведенном выше векторном поле одно и то же в любой точке (x,y). График ротора F не слишком интересен:
Более сложный пример
Теперь рассмотрим несколько более сложное векторное поле:
 .
.
Его график:
Мы можем не увидеть никакого вращения, но, посмотрев повнимательнее направо, мы видим большее поле в, например, точке x=4, чем в точке x=3. Если бы мы установили маленькое колесо с лопастями там, больший поток на правой стороне заставил бы колесо вращаться по часовой стрелке, что соответствует ввинчиванию в направлении —z. Если бы мы расположили колесо в левой части поля, больший поток на его левой стороне заставил бы колесо вращаться против часовой стрелке, что соответствует ввинчиванию в направлении +z. Проверим нашу догадку с помощью вычисления:
Действительно, ввинчивание происходит в направлении +z для отрицательных x и —z для положительных x, как и ожидалось. Так как этот ротор не одинаков в каждой точке, его график выглядит немного интереснее:
Ротор F с плоскостью x=0, выделенной темно-синим цветом
Можно заметить, что график этого ротора не зависит от y или z (как и должно быть) и направлен по —z для положительных x и в направлении +z для отрицательных x.
Три общих примера
Рассмотрим пример ∇ × [ v × F ]. Используя прямоугольную систему координат, можно показать, что
Если v и ∇ поменять местами:
что является фейнмановской записью с нижним индексом ∇F, что значит, что градиент с индексом F относится только к F.
Другой пример ∇ × [ ∇ × F ]. Используя прямоугольную систему координат, можно показать, что:
что можно считать частным случаем первого примера с подстановкой v → ∇.
Поясняющие примеры
- В смерче ветры вращаются вокруг центра, и векторное поле скоростей ветра имеет ненулевой ротор везде. (см. Вихревое движение).
- В векторном поле, описывающем линейные скорости движения каждой точки вращающегося диска ротор был бы постоянным во всех частях диска.
- Если бы скорости автомобилей на трассе описывались векторным полем, и разные полосы имели разные ограничения по скорости движения, ротор на границе между полосами был бы ненулевым.
- Закон электромагнитной индукции Фарадея, одно из уравнений Максвелла, может быть выражен очень просто через понятие ротора. Он говорит, что ротор электрического поля равен скорости изменения магнитного поля, взятой с обратным знаком, а ротор напряжённости магнитного поля равен сумме плотностей тока обычного и тока смещения.
[1]
Примечания
- ↑ Математический словарь высшей школы. В. Т. Воднев, А. Ф. Наумович, Н. Ф. Наумович
См. также
Wikimedia Foundation. 2010.
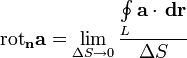 .
.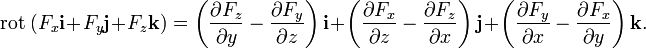
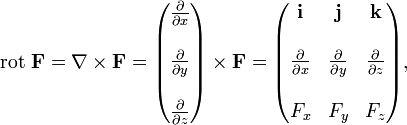
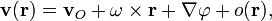
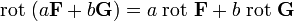
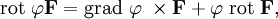
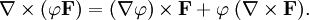
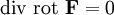 или
или 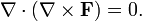
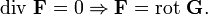
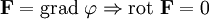
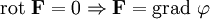
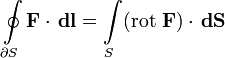
![\operatorname{rot}\;\mathbf{A} = \operatorname{rot}\;(\mathbf{q_1}A_1 + \mathbf{q_2}A_2 + \mathbf{q_3}A_3) = \frac{1}{H_2H_3}\left[\frac{\partial}{\partial q_2}(A_3H_3) - \frac{\partial}{\partial q_3}(A_2H_2)\right]\mathbf{q_1} +](/800/600/https/dic.academic.ru/pictures/wiki/files/102/ffb673a3dba35b73ce0df468756ec0c3.png)
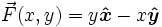 .
.![\vec{\nabla} \times \vec{F} =0\boldsymbol{\hat{x}}+0\boldsymbol{\hat{y}}+ [{\frac{\partial}{\partial x}}(-x) -{\frac{\partial}{\partial y}} y]\boldsymbol{\hat{z}}=-2\boldsymbol{\hat{z}}](/800/600/https/dic.academic.ru/pictures/wiki/files/51/308266a9235d72638006c5b51bd0faea.png)
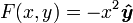 .
.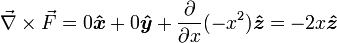
![\mathbf{ \nabla \times} \left( \mathbf{v \times F} \right) = \left[ \left( \mathbf{ \nabla \cdot F } \right) + \mathbf{F \cdot \nabla} \right] \mathbf{v}- \left[ \left( \mathbf{ \nabla \cdot v } \right) + \mathbf{v \cdot \nabla} \right] \mathbf{F} \ .](/800/600/https/dic.academic.ru/pictures/wiki/files/50/2628b53319924465c2409f2d3b024ef5.png)