Крутящий момент единицы измерения – Перевод единиц измерения Крутящего момента. Единицы момента силы, единицы вращательного момента, единицы вертящего момента, единицы вращающего момента. Таблица.
Момент силы — Википедия
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Моме́нт си́лы (синонимы: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы и вектора этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:
- M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}
где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы (в предположении, что ось вращения проходит через начало координат).
Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.
Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.
Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.
Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.
Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=π2−α{\displaystyle \beta ={\frac {\pi }{2}}-\alpha }, а так как cos(π2−α)=sinα{\displaystyle \cos {\left({\frac {\pi }{2}}-\alpha \right)}=\sin \alpha }, получаем, что |F→|cosβ=|F→|sinα{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.
Теперь запишем бесконечно малую работу через новые равенства: dA=|r→|dφ|F→|sinα{\displaystyle dA=\left|{\vec {r}}\right|d\varphi \left|{\vec {F}}\right|\sin \alpha }, или dA=|r→||F→|sin(α)dφ{\displaystyle dA=\left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin(\alpha )d\varphi }.
Теперь видно, что произведение |r→||F→|sinα{\displaystyle \left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin \alpha } есть не что иное, как модуль векторного произведения векторов r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}}, то есть |r→×F→|{\displaystyle \left|{\vec {r}}\times {\vec {F}}\right|}, которое и было принято обозначить за момент силы M{\displaystyle M}, или модуль вектора момента силы |M→|{\displaystyle \left|{\vec {M}}\right|}.
Теперь полная работа записывается просто: A=∫0φ|r→×F→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {r}}\times {\vec {F}}\right|d\varphi }, или A=∫0φ|M→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {M}}\right|d\varphi }.
Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Энергия и механическая работа также имеют размерность «сила, умноженная на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина псевдовекторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоуля. Математически:
- E=Mθ,{\displaystyle E=M\theta ,}
где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.
Формула момента рычага[править | править код]
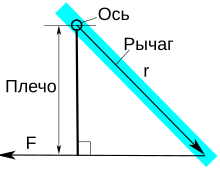 Момент, действующий на рычаг
Момент, действующий на рычагОчень интересен особый случай, представляемый как определение момента силы в поле:
- |M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}
где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:
- |T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}
Сила под углом[править | править код]
Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsinθ{\displaystyle M=rF\sin \theta }.
Статическое равновесие[править | править код]
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0,ΣV=0{\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM=0{\displaystyle \Sigma M=0}.
Момент силы как функция от времени[править | править код]
Момент силы — производная по времени от момента импульса,
Видеоурок: вращающий момент- M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}
где L→{\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- Lo→=Icω→+[M(ro→−rc→),vc→].{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+[M({\vec {r_{o}}}-{\vec {r_{c}}}),{\vec {v_{c}}}].}
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то
- M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}
где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
- Mc→=Icdω→dt+[w→,Icw→].{\displaystyle {\vec {M_{c}}}=I_{c}{\frac {d{\vec {\omega }}}{dt}}+[{\vec {w}},I_{c}{\vec {w}}].}
Отношение между моментом силы и мощностью[править | править код]
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Так же и момент силы, если совершает действие через угловое расстояние, он совершает работу.
- P=M→⋅ω→.{\displaystyle P={\vec {M}}\cdot {\vec {\omega }}.}
В системе СИ мощность P{\displaystyle P} измеряется в ваттах, момент силы — в ньютоно-метрах, а угловая скорость — в радианах в секунду.
Отношение между моментом силы и работой[править | править код]
- A=∫θ1θ2|M→|dθ.{\displaystyle A=\int _{\theta _{1}}^{\theta _{2}}\left|{\vec {M}}\right|\mathrm {d} \theta .}
В случае постоянного момента получаем:
- A=|M→|θ.{\displaystyle A=\left|{\vec {M}}\right|\theta .}
В системе СИ работа A{\displaystyle A} измеряется в джоулях, момент силы — в ньютоно-метрах, а угол — в радианах.
Обычно известна угловая скорость ω{\displaystyle \omega } в радианах в секунду и время действия момента t{\displaystyle t}.
Тогда совершённая моментом силы работа рассчитывается как:
- A=|M→|ωt.{\displaystyle A=\left|{\vec {M}}\right|\omega t.}
Если имеется материальная точка OF{\displaystyle O_{F}}, к которой приложена сила F→{\displaystyle {\vec {F}}}, то момент силы относительно точки O{\displaystyle O} равен векторному произведению радиус-вектора r→{\displaystyle {\vec {r}}}, соединяющего точки O{\displaystyle O} и OF{\displaystyle O_{F}}, на вектор силы F→{\displaystyle {\vec {F}}}:
- MO→=[r→×F→].{\displaystyle {\vec {M_{O}}}=\left[{\vec {r}}\times {\vec {F}}\right].}
Момент силы относительно оси равен алгебраическому значению проекции момента этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть
- Mz(F)=Mo(F′)=F′h′.{\displaystyle M_{z}(F)=M_{o}(F’)=F’h’.}
Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными,
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Алфавиты, номиналы, единицы / / Перевод единиц измерения величин. Перевод единиц измерения физических величин. Таблицы перевода единиц величин. Перевод химических и технических единиц измерения величин. Величины измерения. Таблицы соответствия величин. / / Перевод единиц измерения Крутящего момента. Единицы момента силы, единицы вращательного момента, единицы вертящего момента, единицы вращающего момента. Таблица. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор Крутящий момент | Преобразование единиц крутящего момента
Крутящий момент, момент силы — направленность сил на осуществление поворота объекта вокруг оси или точки опоры. В математике крутящий момент определяется как векторное производное расстояния и силы, которой свойственно производить вращение. Проще говоря, крутящий момент — это мера силы вращения объекта, такого как маховик или болт. Как правило, символ — греческая буква Тау (Т) или иногда обозначается буквой «М», от слова «момент». Единицей СИ для крутящего момента является ньютон-метр (Н•м). Единицы фунт-сила-фут, фунт-сила-дюйм и унция-сила-фут также используются для крутящего момента. Для всех этих величин слово «сила» часто выпадает, к примеру, фунт-сила-дюйм сокращается до «фунт-дюйм».
Конвертер крутящего момента
Переводим из
Переводим в
| Основные единицы | |
| Килоньютон на метр | кН·м |
| Ньютон на метр | Н·м |
| Фунт-Сила-Дюйм | lbf∙in |
| Другие единицы | |
| Дина-сантиметр | дин·см |
| Дина-Метр | дин·м |
| Дина-Миллиметр | дин·мм |
| Грамм-Сила-Сантиметр | гс·см |
| Грамм-Сила-Метр | гс·м |
| Грамм-Сила-Миллиметр | гс·мм |
| Килограмм-Сила-Сантиметр | кгс∙см |
| Килограмм-Сила-Метр | кгс∙м |
| Килограмм-Сила-Миллиметр | кгс∙мм |
| Ньютон сантиметр | Н∙cм |
| Ньютон-Миллиметр | Н∙мм |
| Унция-Сила-Дюйм | ozf∙in |
| Основные единицы | |
| Килоньютон на метр | кН·м |
| Ньютон на метр | Н·м |
| Фунт-Сила-Дюйм | lbf∙in |
| Другие единицы | |
| Дина-сантиметр | дин·см |
| Дина-Метр | дин·м |
| Дина-Миллиметр | дин·мм |
| Грамм-Сила-Сантиметр | гс·см |
| Грамм-Сила-Метр | гс·м |
| Грамм-Сила-Миллиметр | гс·мм |
| Килограмм-Сила-Сантиметр | кгс∙см |
| Килограмм-Сила-Метр | кгс∙м |
| Килограмм-Сила-Миллиметр | кгс∙мм |
| Ньютон сантиметр | Н∙cм |
| Ньютон-Миллиметр | Н∙мм |
| Унция-Сила-Дюйм | ozf∙in |
Результат конвертации:
определения, единица измерения, примеры, относительно оси и точки
В статье мы расскажем про момент силы относительно точки и оси, определения, рисунки и графики, какая единица измерения момента силы, работа и сила во вращательном движении, а также примеры и задачи.
Момент силы представляет собой вектор физической величины, равный произведению векторов плеча силы (радиус-вектор частицы) и силы, действующей на точку. Силовой рычаг представляет собой вектор, соединяющий точку, через которую проходит ось вращения твердого тела с точкой, к которой приложена сила.

где: r — плечо силы, F — сила приложенная на тело.
Направление вектора силы момента всегда перпендикулярно плоскости, определяемой векторами r и F.
Главный момент — любая система сил на плоскости относительно принятого полюса называется алгебраическим моментом момента всех сил этой системы относительно этого полюса.
Во вращательных движениях важны не только сами физические величины, но и то, как они расположены относительно оси вращения, то есть их моменты. Мы уже знаем, что во вращательном движении важна не только масса, но и момент инерции. В случае силы, ее эффективность для запуска ускорения определяется способом приложения этой силы к оси вращения.

Взаимосвязь между силой и способом ее применения описывает МОМЕНТ СИЛЫ. Момент силы — это векторное произведение силового плеча R на вектор силы F:


Как в каждом векторном произведении, так и здесь



Следовательно, сила не будет влиять на вращение, когда угол между векторами силы F и рычагом R равен 0o или 180o. Каков эффект применения момента силы М?
Мы используем второй Закон движения Ньютона и связь между канатом и угловой скоростью v = Rω в скалярной форме, действительны, когда векторы R и ω перпендикулярны друг другу

Умножив обе части уравнения на R, получим

Поскольку mR 2 = I, мы заключаем, что

Вышеуказанная зависимость справедлива и для случая материального тела. Обратите внимание, что в то время как внешняя сила дает линейное ускорение a, момент внешней силы дает угловое ускорение ε.

Единица измерения момента силы
Основной мерой измерения момента силы в системной координате СИ является: [M]=Н•м
В СГС: [M]=дин•см
Работа и сила во вращательном движении
Работа в линейном движении определяется общим выражением,

но во вращательном движении,

а следовательно

Исходя из свойств смешанного произведения трех векторов, можно записать

Поэтому мы получили выражение для работы во вращательном движении:

Мощность во вращательном движении:

Момент силы пример и решение задач относительно точки
Найдите момент силы, действующей на тело в ситуациях, показанных на рисунках ниже. Предположим, что r = 1m и F = 2N.

а) поскольку угол между векторами r и F равен 90°, то sin(a)=1:
M = r • F = 1м • 2N = 2Н • м
б) потому что угол между векторами r и F равен 0°, поэтому sin(a)=0:
M = 0
да направленная сила не может дать точке вращательное движение.
c) поскольку угол между векторами r и F равен 30°, то sin(a)=0.5:
M = 0,5 r • F = 1Н • м.
Таким образом, направленная сила вызовет вращение тела, однако ее эффект будет меньше, чем в случае a).
Момент силы относительно оси
Предположим, что данные являются точкой O (полюс) и мощность P. В точке O мы принимаем начало прямоугольной системы координат. Момент силы Р по отношению к полюсным O представляет собой вектор М из (Р), (рисунок ниже).

Любая точка A на линии P имеет координаты (xo , yo , zo ).
Вектор силы P имеет координаты Px , Py, Pz. Комбинируя точку A (xo, yo, zo ) с началом системы, мы получаем вектор p. Координаты вектора силы P относительно полюса O обозначены символами Mx, My, Mz. Эти координаты могут быть вычислены как минимумы данного определителя, где ( i, j, k) — единичные векторы на осях координат (варианты): i, j, k

После решения определителя координаты момента будут равны:

Координаты вектора моментов Mo (P) называются моментами силы относительно соответствующей оси. Например, момент силы P относительно оси Oz окружает шаблон:
Mz = Pyxo — Pxyo
Этот паттерн интерпретируется геометрически так, как показано на рисунке ниже.

На основании этой интерпретации момент силы относительно оси Oz можно определить, как момент проекции силы P на перпендикуляр оси Oz относительно точки проникновения этой плоскости осью. Проекция силы P на перпендикуляр оси обозначена Pxy, а точка проникновения плоскости Oxy — осью Oс символом O.
Из приведенного выше определения момента силы относительно оси следует, что момент силы относительно оси равен нулю, когда сила и ось равны, в одной плоскости (когда сила параллельна оси или когда сила пересекает ось).
Используя формулы на Mx, My, Mz, мы можем рассчитать значение момента силы P относительно точки O и определить углы, содержащиеся между вектором M и осями системы:

Если сила лежит в плоскости Oxy, то zo = 0 и Pz = 0 (см. Рисунок ниже).

Момент силы P по отношению к точке (полюсу) O составляет:
Mx = 0,
My = 0,
Mo (P) = Mz = Pyxo — Pxyo.

Метка крутящего момента:
плюс (+) — вращение силы вокруг оси O по часовой стрелке,
минус (-) — вращение силы вокруг оси O против часовой стрелки.
Ньютон-метр — Википедия
Материал из Википедии — свободной энциклопедии
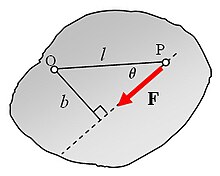 Момент силы F относительно точки О равен F.b, пунктир — линия действия силы.
Момент силы F относительно точки О равен F.b, пунктир — линия действия силы.Ньютон-метр (русское обозначение Н·м; международное: N·m) — единица измерения момента силы в Международной системе единиц (СИ). Один ньютон-метр равен моменту силы, создаваемому силой, равной 1 Н, относительно точки, расположенной на расстоянии 1 м от линии действия силы.
По правилам форматирования, принятым в СИ, буквенные обозначения единиц, входящих в произведение, разделяются точкой на средней линии (знаком умножения). Допускается также разделять их пробелом, если это не может вызвать недоразумения. Символ «х» для этих целей не используется[1].
За основу единицы был принят ньютон.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Н·м | деканьютон-метр | даН·м | daN·m | 10−1 Н·м | дециньютон-метр | дН·м | dN·m |
| 102 Н·м | гектоньютон-метр | гН·м | hN·m | 10−2 Н·м | сантиньютон-метр | сН·м | cN·m |
| 103 Н·м | килоньютон-метр | кН·м | kN·m | 10−3 Н·м | миллиньютон-метр | мН·м | mN·m |
| 106 Н·м | меганьютон-метр | МН·м | MN·m | 10−6 Н·м | микроньютон-метр | мкН·м | µN·m |
| 109 Н·м | гиганьютон-метр | ГН·м | GN·m | 10−9 Н·м | наноньютон-метр | нН·м | nN·m |
| 1012 Н·м | тераньютон-метр | ТН·м | TN·m | 10−12 Н·м | пиконьютон-метр | пН·м | pN·m |
| 1015 Н·м | петаньютон-метр | ПН·м | PN·m | 10−15 Н·м | фемтоньютон-метр | фН·м | fN·m |
| 1018 Н·м | эксаньютон-метр | ЭН·м | EN·m | 10−18 Н·м | аттоньютон-метр | аН·м | aN·m |
| 1021 Н·м | зеттаньютон-метр | ЗН·м | ZN·m | 10−21 Н·м | зептоньютон-метр | зН·м | zN·m |
| 1024 Н·м | иоттаньютон-метр | ИН·м | YN·m | 10−24 Н·м | иоктоньютон-метр | иН·м | yN·m |
| применять не рекомендуется | |||||||
1 килограмм-сила-метр (кгс·м; kp·m, Kilopond · Meter) = 9,80665 Н·м
1 кгс·см, kp·cm = 0,0980665 Н·м
1 дюйм-унция-сила = 7,0615518 мН·м
1 дина-сантиметр = 10−7 Н·м
0,7375621 ft·lb (Foot-pound) = 1 Н·м
1 ft·lb = 1,3558179483314004 Н·м
Вращающий момент — это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
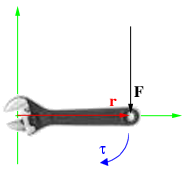
Момент силы приложенный к гаечному ключу
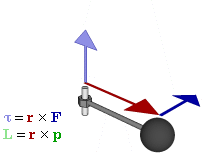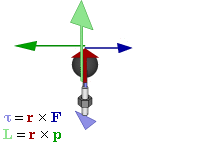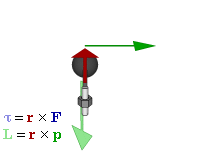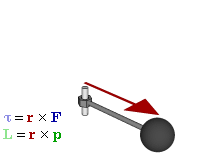
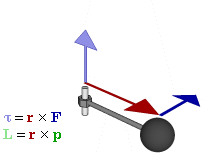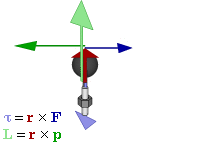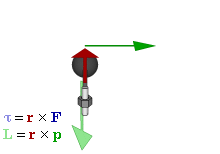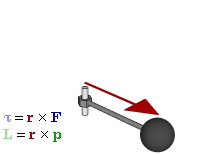
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
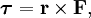
где 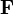 — сила, действующая на частицу, а
— сила, действующая на частицу, а 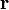 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 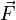 на рычаг
на рычаг 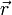 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 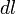 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 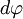 . Обозначим через
. Обозначим через 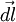 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 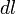 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы 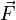 и вектором
и вектором 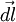 равен
равен 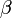 , а угол
, а угол 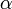
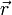 и вектором силы
и вектором силы 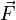 .
.
Следовательно, бесконечно малая работа 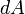 , совершаемая силой
, совершаемая силой 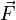 на бесконечно малом участке
на бесконечно малом участке 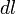 равна скалярному произведению вектора
равна скалярному произведению вектора 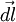 и вектора силы, то есть
и вектора силы, то есть 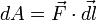 .
.
Теперь попытаемся выразить модуль вектора 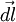 через радиус вектор
через радиус вектор 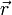 , а проекцию вектора силы
, а проекцию вектора силы 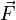 на вектор
на вектор 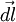 , через угол
, через угол 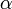 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 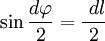 , где в случае малого угла справедливо
, где в случае малого угла справедливо 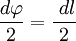 и следовательно
и следовательно 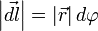
Для проекции вектора силы 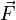 на вектор
на вектор 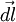 , видно, что угол
, видно, что угол 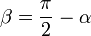 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 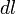 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу 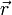 , а так как
, а так как 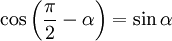 , получаем, что
, получаем, что 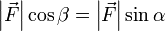 .
.
Теперь запишем бесконечно малую работу через новые равенства 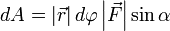 или
или 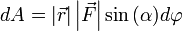 .
.
Теперь видно, что произведение 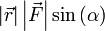 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 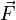 и
и 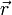 , то есть
, то есть 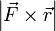 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 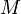 или модуля вектора момента силы
или модуля вектора момента силы 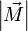 .
.
И теперь полная работа записывается очень просто 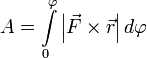 или
или 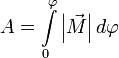 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
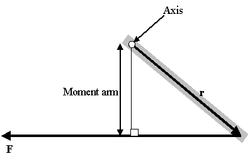
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 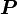 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 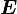 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 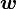 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 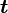 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 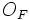 , к которой приложена сила
, к которой приложена сила 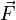 , то момент силы относительно точки
, то момент силы относительно точки 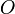 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 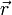 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 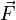 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/dic.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Крутящий момент — это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы приложенный к гаечному ключу

Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
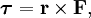
где 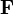 — сила, действующая на частицу, а
— сила, действующая на частицу, а 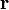 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 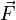 на рычаг
на рычаг 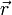 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 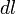 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 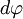 . Обозначим через
. Обозначим через 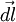 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 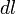 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы 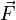 и вектором
и вектором 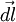 равен
равен 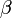 , а угол
, а угол 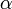
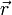 и вектором силы
и вектором силы 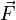 .
.
Следовательно, бесконечно малая работа 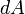 , совершаемая силой
, совершаемая силой 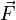 на бесконечно малом участке
на бесконечно малом участке 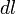 равна скалярному произведению вектора
равна скалярному произведению вектора 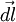 и вектора силы, то есть
и вектора силы, то есть 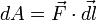 .
.
Теперь попытаемся выразить модуль вектора 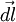 через радиус вектор
через радиус вектор 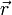 , а проекцию вектора силы
, а проекцию вектора силы 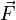 на вектор
на вектор 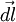 , через угол
, через угол 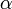 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 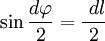 , где в случае малого угла справедливо
, где в случае малого угла справедливо 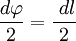 и следовательно
и следовательно 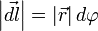
Для проекции вектора силы 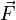 на вектор
на вектор 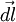 , видно, что угол
, видно, что угол 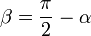 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 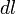 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу 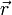 , а так как
, а так как 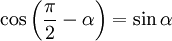 , получаем, что
, получаем, что 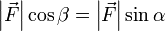 .
.
Теперь запишем бесконечно малую работу через новые равенства 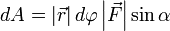 или
или 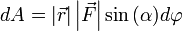 .
.
Теперь видно, что произведение 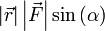 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 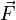 и
и 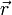 , то есть
, то есть 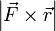 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 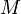 или модуля вектора момента силы
или модуля вектора момента силы 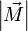 .
.
И теперь полная работа записывается очень просто 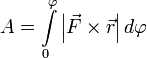 или
или 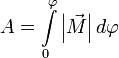 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага

Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 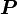 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 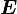 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 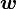 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 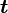 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 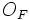 , к которой приложена сила
, к которой приложена сила 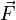 , то момент силы относительно точки
, то момент силы относительно точки 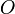 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 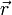 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 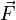 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/dic.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
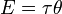 ,
,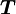 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ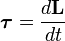 ,
,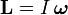 ,
,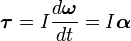 ,
,