Автомобиль начинает двигаться от точки влево проверь верно ли записан – 12 хитростей для начинающих водителей, о которых не рассказывают в автошколе

(русский язык) — Диагностическая работа 1 (начало учебного года) 1

---

С этим файлом связано 42 файл(ов). Среди них: fokina_l-p-zaglavnaja_bukva.ppsx, vospitanie_nenasilija_v_seme.docx, vospitanie_nenasilija.ppt, vkhodnaja_diagnostika_1_kl.doc, tekhnologija_3_klass.doc, tablica_umnozhenija.ppt, sto_slov.doc, stalingrad_kl.chas.doc, sonata-pro-konstruktor_rabochikh_programm.rar, samopredstavlenie_svoego_opyta.docx и ещё 32 файл(а).
Показать все связанные файлы

---

Диагностическая работа № 1 (начало учебного года)

1 вариант
Фамилия, имя _______________________________________
1. Отметь только верные записи.
□ 5 + 9 = 15

□ 6 – 0 = 0

□ 7 + 6 = 13

□ 0 + 1 = 0

□ 10 – 3 = 7
2. Распредели записи по группам двумя разными способами.

7 + 2 12 – 3 5 + 3 10 – 2
Способ 1 Способ 2

3. Отметь только верные записи.
□ 17 меньше 18 на 1

□ 8 больше 6 на 3

□ 15 больше 16 на 1

□ 8 меньше 11 на 3
4. Прочитай условие задачи.

В книге 16 страниц. Петя начал читать её утром, а закончил вечером. Утром Петя прочитал 6 страниц, днём – 4 страницы.
Отметь вопросы, на которые можно ответить по данному условию.

□ Сколько страниц Петя прочитал утром и днём?

□ На сколько больше страниц Петя прочитал утром, чем днём?

□ Сколько страниц этой книги Петя прочитал вчера?

□ Сколько страниц Петя прочитал вечером?
5. Ответь на вопрос задачи.

На уроке физкультуры друг за другом бегут 10 учеников. Саша бежит третьим, а Дима бежит девятым. Сколько учеников бегут между ними?
Ответ: ____ учеников.

Объясни свой ответ. Сделай схематический рисунок.

6. В каждой группе подчеркни «лишнее» слово или число.

треугольник, пятиугольник, круг, квадрат

умножение, сложение, вычитание, выражение

18, 20, 15, 3, 19
7. Нарисуй справа вазу так, чтобы в неё можно было положить конфеты.

8. Автомобиль начинает двигаться от точки влево. Проверь, верно ли записан «путь» автомобиля.
Отметь неверные записи.

9. Сколько треугольников ты видишь в этой фигуре?
Ответ: ____ треугольников.
Диагностическая работа № 1 (начало учебного года)

2 вариант
Фамилия, имя _______________________________________
1. Отметь только верные записи.
□ 10 – 4 = 6

□ 1 – 0 = 0

□ 3 + 9 = 13

□ 8 + 7 = 15

□ 0 + 2 = 0
2. Распредели записи по группам двумя разными способами.

5 + 3 14 – 3 7 + 4 12 – 4
Способ 1 Способ 2

3. Отметь только верные записи.
□ 13 больше 14 на 1

□ 15 меньше 16 на 1

□ 9 меньше 11 на 2

□ 9 больше 7 на 3
4. Прочитай условие задачи.

В книге 18 страниц. Аня начала читать её утром и закончила вечером. Утром она прочитала 5 страниц, днём – 3 страницы.
Отметь вопросы, на которые можно ответить по данному условию.

□ На сколько страниц меньше Аня прочитала днём, чем утром?

□ Сколько страниц Аня прочитает завтра?

□ Сколько страниц Аня прочитала утром и днём?

□ Сколько страниц Аня прочитала вечером?
5. Ответь на вопрос задачи.

По тропинке друг за другом идут 10 детей. Миша идёт вторым. А Коля идёт седьмым. Сколько детей идут между ними?
Ответ: ____ детей.

Объясни свой ответ. Сделай схематический рисунок.

6. В каждой группе подчеркни «лишнее» слово или число.

квадрат, треугольник, отрезок, пятиугольник

деление, сложение, упражнение, вычитание

9, 8, 6, 11, 5
7. Нарисуй справа вазу так, чтобы в неё можно было положить конфеты.

8. Автомобиль начинает двигаться от точки влево. Проверь, верно ли записан «путь» автомобиля.
Отметь неверные записи.

9. Сколько треугольников ты видишь в этой фигуре?
Ответ: ____ треугольников.
перейти в каталог файлов

Задачи на движение. ЕГЭ по математике. Разбор задач.

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Если прочитаешь эту статью — гарантирую — ты научишься решать задачи на движение.

И вообще… умение решать задачи на движение может перевесить чашу весов в ту или иную сторону…сдашь ты экзамен или нет… поступишь на бюджет или нет…

В общем, думаю, никого убеждать не надо. Читай эту статью и РЕШАЙ ЗАДАЧИ!

Let’s dive right in… (Поехали!) 

Без чего нельзя решать задачи на движение (или без чего трудно хорошо сдать ЕГЭ по математике!) 

Для успешного решения задач на движение нужно все время держать в голове одну простую формулу:

Чтобы легче запомнить эту формулу, подумай, что ты ответишь на такой вопрос:

«Сколько километров я проеду на велосипеде за   часа, двигаясь со скоростью   км/ч?»

Ты, не задумываясь, ответишь –   км. Ну вот. Поздравляю! Эту формулу ты всегда хорошо знал, просто не мог сформулировать.

Из нашей формулы легко выразить все ее составляющие:

Очень многим запомнить формулу помогает вот такая пирамидка:

Усвоил? А теперь рассмотрим подробный алгоритм решения задачна движение. Он состоит из   больших этапов.

Разберем немного подробнее некоторые особенности и тонкости, возникающие при решении задач на движение.

Немного о внимательности в прочтении задач на движение

Прочитай задачу несколько раз. Осознай ее настолько, чтобы тебе было понятно абсолютно все.

Например, часто возникают трудности с понятием «собственная скорость лодки/катера» и т.д.

Подумай, что это может значить? Правильно, скорость лодки в стоячей воде, например, в пруду, когда на нее НЕ влияет скорость течения.

Кстати, в задачах иногда пишут «найти скорость лодки в стоячей воде».

Теперь ты знаешь, что собственная скорость лодки и скорость лодки в стоячей воде – одно и тоже, так что не теряйся, если встретишь оба этих определения.

Кто куда едет, кто к кому приехал, и где они все встретились

Сделай рисунок, попутно записывая на нем все известные величины (ну либо под ним, если не знаешь, как их отобразить схематически).

Рисунок должен четко отражать весь смысл задачи. Его следует сделать таким образом, чтобы на нем была видна динамика движения – направления движения, встречи, развороты, повороты.

Качественный рисунок позволяет понять задачу, не заглядывая в ее текст. Он – твоя основная подсказка для дальнейшего составления уравнения.

Рассмотрим возможные виды движения двух тел…

Не веришь? Давай посмотрим на практике.

Допустим, из точки   и из точки   навстречу друг другу выехали две машины. Скорость одной машины –   км/ч, а скорость   машины –   км/ч. Они встретились через   часа. Какое расстояние между пунктами   и  ?

Просто второе более рационально, так что запоминай формулу (она абсолютно логична, правда?), а для усвоения реши следующую задачу:

Оба решения являются верными.

Миша и Вася ехали на велосипеде навстречу друг к другу. Скорость Миши-  км/ч, скорость Васи –   км/ч. Ребята встретились через   часа. Какой совместный путь они проделали?

Решил? У меня получилось, что скорость сближения равна   км/ч, а путь равен   км.

Теперь разберемся, как вычисляется время при подобном случае

Исходя из предыдущей формулы, это вполне логично, однако, попробуем проверить на практике.

Итак, задача – Из пункта   и пункта   машины движутся навстречу друг другу со скоростями   км/ч и   км/ч. Расстояние между пунктами –   км. Через сколько времени машины встретятся?

Пусть   – время, которое едут машины, тогда путь первой машины –  , а путь второй машины –  .

Их сумма и будет равна расстоянию между пунктами   и   —  .

  (ч) – время, через которое встретились машины.

Попробуй самостоятельно решить задачу и доказать верность данной формулы как в предыдущем случае.

Из Москвы в противоположные стороны выехало   машины. Скорость одной машины –   км/ч, скорость другой –   км/ч. На каком расстоянии друг от друга будут находиться машины через   часа?

Решая первым способом, у меня получилось, что путь, проделанный первой машиной, равен   км, а второй –   км. Соответственно, расстояние между машинами –   км.

Решая вторым способом, выходит, что скорость удаления равна \displaystyle 145  км/ч, а путь равен \displaystyle 145  км/ч   = \displaystyle 290 км.

Теперь разберемся, как вычисляется время при подобном случае.

Как ты видишь, формула, аналогичная выведенной нами при

движении тел навстречу друг другу. Считаешь, что такого не может быть? Проверь ее на практике!

Допустим, что две машины двигаются в противоположных направлениях со скоростями   и   км/ч. При остановке, расстояние между ними составляло   км. Сколько времени ехали машины?

Попробуй решить эту задачу теми двумя способам, которые были описаны при движении на встречу.

Решил? Формула подтвердилась? Давай сравнивать ответы.

Уравнение, получаемое при решении 1 вариантом —  ; при решении 2 вариантом — скорость удаления –   км/ч, время в пути –   часа.

А что если, тела изначально находятся на неком расстоянии   друг от друга? Это выглядит примерно так:

Как решать подобные задачи тогда? Очень просто. При решении нам необходимо обязательно учитывать  .

Логично? Вырази из этой формулы время встречи двух тел, а потом сравним что у нас получилось.

Справился? Тогда решим задачу на данную формулу.

Из разных точек города N в стороны, противоположные друг другу, выехало два мотоциклиста. Изначальное расстояние между ними составляло   км. Скорость первого мотоциклиста составляла   км/ч; скорость второго –   км/ч.

Через какое время расстояние между ними будет равно   км?

Какой ответ ты получил? У меня получилось   часа.

Давай проверим все обстоятельно. Путь, который мотоциклисты действительно ехали равен  км км км. Скорость их удаления друг от друга равна   км/ч.

Делим   км на   км/ч и получаем   часа – время, которое мотоциклисты провели в дороге.

 

Итак, допустим, наши тела двигаются в одном направлении. Как ты думаешь, сколько случаев может быть для такого условия? Правильно, два.

Почему так получается? Уверена, что после всех примеров ты с легкостью сам разберешься, как вывести данные формулы.

Разобрался? Молодец! Пришло время решить задачу.

Четвертая задача

Коля едет на работу на машине со скоростью   км/ч. Коллега Коли Вова едет со скоростью   км/ч. Коля от Вовы живет на расстоянии   км.

Через сколько времени Вова догонит Колю, если из дома они выехали одновременно?

Посчитал? Сравним ответы – у меня получилось, что Вова догонит Колю через   часа или через   минут.

Сравним наши решения…

Рисунок выглядит вот таким образом:

Похож на твой? Молодец!

Так как в задаче спрашивается, через сколько ребята встретились, а выехали они одновременно, то время  , которое они ехали, будет одинаковым, так же как место встречи   (на рисунке оно обозначено точкой  ). Составляя уравнения, возьмем время за  .

Итак, Вова до места встречи проделал путь  . Коля до места встречи проделал путь  . Это понятно. Теперь разбираемся с осью передвижения.

Начнем с пути, который проделал Коля. Его путь ( ) на рисунке изображен как отрезок  . А из чего состоит путь Вовы ( )? Правильно, из суммы отрезков   и  , где   – изначальное расстояние между ребятами, а   равен пути, который проделал Коля.

Исходя из этих выводов, получаем уравнение:

 

Разобрался? Если нет, просто прочти это уравнение еще раз и посмотри на точки, отмеченные на оси. Рисунок помогает, не правда ли?

Решаем дальше и получаем:

 

 

  часа или   минут   минут.

Надеюсь, на этом примере ты понял, насколько важную роль играет грамотно составленный рисунок!

А мы плавно переходим, точнее, уже перешли к следующему пункту нашего алгоритма – приведение всех величин к одинаковой размерности.

 

Правило трех «Р» — размерность, разумность, расчет.

Размерность.

Далеко не всегда в задачах дается одинаковая размерность для каждого участника движения (как это было в наших легких задачках).

Например, можно встретить задачи, где сказано, что тела двигались определенное количество минут, а скорость их передвижения указана в км/ч.

Мы не можем просто взять и подставить значения в формулу – ответ получится неверный. Даже по единицам измерения наш ответ «не пройдет» проверку на разумность. Сравни:

Видишь? При грамотном перемножении у нас также сокращаются единицы измерения, и, соответственно, получается разумный и верный результат.

А что происходит, если мы не переводим в одну систему измерения? Странная размерность у ответа и  % неверный результат.

Итак, напомню тебе на всякий случай значения основных единиц измерения длины и времени.

  сантиметр =   миллиметров

  дециметр =   сантиметров =   миллиметров

  метр =   дециметров =   сантиметров =   миллиметров

  километр =   метров

  минута =   секунд

  час =   минут =   секунд

  сутки =   часа =   минут =   секунд

Совет: Переводя единицы измерения, связанные с временем (минуты в часы, часы в секунды и т.д.) представь в голове циферблат часов. Невооруженным глазом видно, что   минут это четверть циферблата, т.е.   часа,   минут это треть циферблата, т.е.   часа, а   минута это   часа.

А теперь совсем простенькая задача:

Маша ехала на велосипеде из дома в деревню со скоростью   км/ч на протяжении   минут. Какое расстояние между машиным домом и деревней?

Посчитал? Правильный ответ –   км.

  минут – это час, и еще   минут от часа (мысленно представил себе циферблат часов, и сказал, что   минут – четверть часа), соответственно –   мин =   ч.

  км

Разумность.

Ты же понимаешь, что скорость машины не может быть   км/ч, если речь, конечно, идет не о спортивном болиде? И уж тем более, она не может быть отрицательной, верно? Так вот, разумность, это об этом)

Расчет.

Посмотри, «проходит» ли твое решение на размерность и разумность, и только потом проверяй расчеты. Логично же – если с размерностью и разумностью получается несостыковочка, то проще все зачеркнуть и начать искать логические и математические ошибки.

 

«Любовь к таблицам» или «когда рисунка недостаточно»

Далеко не всегда задачи на движение такие простые, как мы решали раньше. Очень часто, для того, чтобы правильно решить задачу, нужно не просто нарисовать грамотный рисунок, но и составить таблицу со всеми данными нам условиями.

Первая задача

Из пункта   в пункт  , расстояние между которыми   км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на   км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт   на   минут позже, чем мотоциклист.

Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать – прямая, пункт  , пункт  , две стрелочки…

В общем рисуй, и сейчас сравним, что у тебя получилось.

Пустовато как-то, правда? Рисуем таблицу.

Как ты помнишь, все задачи на движения состоят из   компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах.

Правда, мы добавим еще один столбец – имя, про кого мы пишем информацию – мотоциклист и велосипедист.

Так же в шапке укажи размерность, в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?

У тебя получилась вот такая таблица?

	Скорость км/ч	Время t, часов	Путь S, км
велосипедист
мотоциклист

 

Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.

Первое, что мы имеем – это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен   км. Вносим!

	Скорость км/ч	Время t, часов	Путь S, км
велосипедист			30
мотоциклист			30

 

Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на   км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста…

Возьмем скорость велосипедиста за  , тогда скорость мотоциклиста будет  …

Если с такой переменной решение задачи не пойдет – ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!

	Скорость км/ч	Время t, часов	Путь S, км
велосипедист			30
мотоциклист			30

 

Таблица преобразилась. У нас осталась не заполнена только одна графа – время. Как найти время, когда есть путь и скорость?

Правильно, разделить путь на скорость. Вноси это в таблицу.

	Скорость км/ч	Время t, часов	Путь S, км
велосипедист			30
мотоциклист			30

 

Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.

Что мы можем на нем отразить?

Молодец. Скорость передвижения мотоциклиста и велосипедиста.

Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.

Какие данные не отражены ни в таблице, ни на рисунке?

Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени –   минут.

Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.

  минут /   минут =   часа.

И что дальше, спросишь ты? А дальше числовая магия!

Магия формул: составление и решение уравнений – манипуляции, приводящие к единственно верному ответу.

Итак, как ты уже догадался, сейчас мы будем составлять уравнение.

Составление уравнения:

Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?

Правильно. Мы можем составить уравнение, основываясь на разнице во времени!

 

Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.

Это уравнение – рациональное. Если не знаешь, что это такое, прочти тему «Рациональные уравнения».

Приводим слагаемые к общему знаменателю:

 

Раскроем скобки и приведем подобные слагаемые:Уф! Усвоил? Попробуй свои силы на следующей задаче.

Решение уравнения:

 

Из этого уравнения мы получаем следующее:

 

 

 

Раскроем скобки и перенесем все в левую часть уравнения:

 

Вуаля! У нас простое квадратное уравнение. Решаем!

 

 

 

 

 

 

 

Мы получили два варианта ответа. Смотрим, что мы взяли за  ? Правильно, скорость велосипедиста.

Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ –   км/ч.

Вторая задача

Два велосипедиста одновременно отправились в  -километровый пробег. Первый ехал со скоростью, на   км/ч большей, чем скорость второго, и прибыл к финишу на   часов раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

Напоминаю алгоритм решения:

• Прочитай задачу пару раз – усвой все-все детали. Усвоил?
• Начинай рисовать рисунок – в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
• Проверь, все ли величины у тебя одинаковой размерности и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь какие там графы?).
• Пока все это пишешь, думай, что взять за  ? Выбрал? Записывай в таблицу! Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок – помни о «3Р»!
• Все сделал? Молодец! У меня получилось, что скорость велосипедиста –   км/ч.

-«Какого цвета твоя машина?» — «Она красивая!» Правильные ответы на поставленные вопросы

Продолжим наш разговор. Так какая там скорость у первого велосипедиста?   км/ч? Очень надеюсь, что ты сейчас не киваешь утвердительно!

Внимательно прочти вопрос: «Какая скорость у первого велосипедиста?»

Понял, о чем я?

Именно! Полученный   – это не всегда ответ на поставленный вопрос!

Вдумчиво читай вопросы — возможно, после нахождения   тебе нужно будет произвести еще некоторые манипуляции, например, прибавить   км/ч, как в нашей задаче.

Еще один момент — часто в задачах все указывается в часах, а ответ просят выразить в минутах, или же все данные даны в км, а ответ просят записать в метрах.

Смотри за размерностью не только в ходе самого решения, но и когда записываешь ответы.

Задачи на движение по кругу

Тела в задачах могут двигаться не обязательно прямо, но и по кругу, например, велосипедисты могут ехать по круговой трассе. Разберем такую задачу.

Задача №1

Из пункта   круговой трассы выехал велосипедист. Через   минут он еще не вернулся в пункт   и из пункта   следом за ним отправился мотоциклист. Через   минут после отправления он догнал велосипедиста в первый раз, а еще через   минут после этого догнал его во второй раз.

Найдите скорость велосипедиста, если длина трассы равна   км. Ответ дайте в км/ч.

Решение задачи №1

Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:

Пусть скорость велосипедиста будет  , а мотоциклиста –  . До момента первой встречи велосипедист был в пути   минут, а мотоциклист –  .

При этом они проехали равные расстояния:

 

Между встречами велосипедист проехал расстояние  , а мотоциклист –  .

Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:

Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили – спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.

Значит,

 

Полученные уравнения решаем в системе:

 

 

Ответ:  .

Разобрался? Попробуй решить самостоятельно следующие задачи:

Задачи для самостоятельной работы:

1. Два мо­то­цик­ли­ста стар­ту­ют од­но­вре­мен­но в одном на­прав­ле­нии из двух диа­мет­раль­но про­ти­во­по­лож­ных точек кру­го­вой трас­сы, длина ко­то­рой равна   км. Через сколь­ко минут мо­то­цик­ли­сты по­рав­ня­ют­ся в пер­вый раз, если ско­рость од­но­го из них на   км/ч боль­ше скорости дру­го­го?
2. Из одной точки кру­го­вой трас­сы, длина ко­то­рой равна   км, од­н­времен­но в одном на­прав­ле­нии стар­то­ва­ли два мотоциклиста. Ско­рость пер­во­го мотоцикла равна   км/ч, и через   минут после стар­та он опе­ре­дил вто­рой мотоцикл на один круг. Най­ди­те ско­рость вто­ро­го мотоцикла. Ответ дайте в км/ч.

Решения задач для самостоятельной работы:

1. Пусть   км/ч — ско­рость пер­во­го мо­то­цик­ли­ста, тогда ско­рость вто­ро­го мо­то­цик­ли­ста равна   км/ч. Пусть пер­вый раз мо­то­цик­ли­сты по­рав­ня­ют­ся через   часов. Для того, чтобы мо­то­цик­ли­сты по­рав­ня­лись, более быст­рый дол­жен пре­одо­леть из­на­чаль­но раз­де­ля­ю­щее их рас­сто­я­ние, рав­ное по­ло­ви­не длины трас­сы.
    
   Получаем, что время равно   часа =   минут.
2. Пусть ско­рость вто­ро­го мотоцикла равна   км/ч. За   часа пер­вый мотоцикл про­шел на   км боль­ше, чем вто­рой, соответственно, получаем уравнение:
    
   Скорость второго мотоциклиста равна   км/ч.

 

Задачи на течение

Теперь, когда ты отлично решаешь задачи «на суше», перейдем в воду, и рассмотрим страаашные задачи, связанные с течением.

Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, – это стоячая вода.

Скорость течения в озере равна  .

Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь – налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести. Это понятно? Логично же.

А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…

Это происходит потому что у реки есть скорость течения, которая относит твой плот по направлению течения.

Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) – он движется со скоростью течения.

Разобрался?

Тогда ответь вот на какой вопрос – «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?

Здесь возможно два варианта.

1-й вариант — ты плывешь по течению.

И тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.

2-й вариант — ты плывешь против течения.

Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы   метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость – скорость течения.

Допустим, тебе надо проплыть   км. Когда ты преодолеешь это расстояние быстрее? Когда ты будешь двигаться по течению или против?

Решим задачку и проверим.

Добавим к нашему пути данные о скорости течения –   км/ч и о собственной скорости плота –   км/ч. Какое время ты затратишь, двигаясь по течению и против него?

Конечно, ты без труда справился с этой задачей! По течению –   час, а против течения аж   часа!

В этом и есть вся суть задач на движение с течением.

Несколько усложним задачу.

Задача №1

Лодка с моторчиком плыла из пункта   в пункт     часа, а обратно –   часа.

Найдите скорость течения, если скорость лодки в стоячей воде –   км/ч

Решение задачи №1

Обозначим расстояние между пунктами, как  , а скорость течения – как  .

Все данные из условия занесем в таблицу:

	Путь S	Скорость v, км/ч	Время t, часов
A –> B (против течения)			3
B –> A (по течению)			2

 

Мы видим, что лодка проделывает один и тот же путь, соответственно:

 

 

 

 

Что мы брали за  ?

Скорость течения. Тогда это и будет являться ответом:)

Скорость течения равна   км/ч.

Задача №2

Байдарка в   вышла из пункта   в пункт  , расположенный в   км от  . Пробыв в пункте    час   минут, байдарка отправилась назад и вернулась в пункт   в  .

Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки   км/ч.

Решение задачи №2

Итак, приступим. Прочитай задачу несколько раз и сделай рисунок. Думаю, ты без труда сможешь решить это самостоятельно.

Все величины у нас выражены в одном виде? Нет. Время отдыха у нас указано и в часах, и в минутах.

Переведем это в часы:

  час   минут =   ч.

Теперь все величины у нас выражены в одном виде. Приступим к заполнению таблицы и поиску того, что мы возьмем за  .

Пусть   – собственная скорость байдарки. Тогда, скорость байдарки по течению равна  , а против течения равна  .

Запишем эти данные, а так же путь (он, как ты понимаешь, одинаков) и время, выраженное через путь и скорость, в таблицу:

	Путь S	Скорость v, км/ч	Время t, часов
Против течения	26
По течению	26

 

Посчитаем, сколько времени байдарка затратила на свое путешествие:

  часов.

Все ли   часов она плыла? Перечитываем задачу.

Нет, не все. У нее был отдых   час   минут, соответственно, из   часов мы вычитаем время отдыха, которое, мы уже перевели в часы:

   ч байдарка действительно плыла.

Догадываешься, что мы делаем дальше? Правильно! Приравниваем полученное время к тому времени, которое мы выразили в таблице через путь и скорость. Получаем:

 

Приведем все слагаемые к общему знаменателю   :

 

Раскроем скобки и приведем подобные слагаемые. Далее решаем получившееся квадратное уравнение. 

С этим, я думаю, ты тоже справишься самостоятельно. Какой ответ у тебя получился? У меня   км/ч.

 

 

Подведем итоги

1. Основная формула:  
   
2. Алгоритм решения задач на движение подразумевает выполнение двух больших этапов:
   
3. В задачах на движение обязательно необходимо рисовать чертеж. Тела могут двигаться навстречу друг другу, в противоположные стороны и догонять друг друга.
4. Все цифры нужно привести в единой размерности – только км или только м; только часы или минуты, и т.д.
5. Решая задачи, удобно записывать данные в виде таблицы с обязательными графами – путь, скорость и время.
6. За   можно брать как то, что нужно найти в задаче, так и другое неизвестное.
7. Внимательно читай, что спрашивается в задаче!   – не всегда ответ. Кроме этого, в ответе могут попросить указать величину в другой единице измерения (не в той, которая вышла у тебя, решая уравнение).
8. Задачи на движение по течению решаются в две формулы:
   

 

ПРОДВИНУТЫЙ УРОВЕНЬ

Задачи на движение. Примеры

Рассмотрим примеры с решениями для каждого типа задач.

Движение с течением

Одни из самых простых задач – задачи на движение по реке. Вся их суть в следующем:

• если движемся по течению, к нашей скорости прибавляется скорость течения;
• если движемся против течения, из нашей скорости вычитается скорость течения.

Пример №1:

Катер плыл из пункта A в пункт B   часов а обратно –   часа. Найдите скорость течения, если скорость катера в стоячей воде   км/ч.

Решение №1:

Обозначим расстояние между пунктами, как AB, а скорость течения – как  .

 

Все данные из условия занесем в таблицу:

	Путь S	Скорость v, км/ч	Время t, часов
A –> B (против течения)	AB	50–x	5
B –> A (по течению)	AB	50+x	3

Для каждой строки этой таблицы нужно записать формулу:

 

 

На самом деле, можно не писать уравнения для каждой из строк таблицы. Мы ведь видим, что расстояние, пройденное катером туда и обратно одинаково.

Значит, расстояние мы можем приравнять. Для этого используем сразу формулу для расстояния:

 .

Часто приходится использовать и формулу для времени:

 .

Пример №2:

Против течения лодка проплывает расстояние в   км на   час дольше, чем по течению. Найдите скорость лодки в стоячей воде, если скорость течения равна   км/ч.

Решение №2 :

Попробуем сразу составить уравнение. Время против течения на   час больше, чем время по течению.

Это записывается так:

 

Теперь вместо каждого времени подставим формулу:

 

Получили обычное рациональное уравнение, решим его:

 

Очевидно, что скорость не может быть отрицательным числом, значит, ответ:   км/ч.

Относительное движение

Если какие-то тела движутся друг относительно друга, часто бывает полезно посчитать их относительную скорость. Она равна:

• сумме скоростей, если тела движутся навстречу друг другу;
• разности скоростей, если тела движутся в одном направлении.

Пример №1

Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями   км/ч и   км/ч. Через сколько минут они встретятся. Если расстояние между пунктами   км?

I способ решения:

 

Относительная скорость автомобилей   км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью   км/ч. Так как между автомобилями изначально расстояние   км, время, через которое второй автомобиль проедет мимо первого:

 .

II способ решения:

Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его  . Тогда первый автомобиль проехал путь  , а второй –  .

В сумме они проехали все   км. Значит,

 .

 

Другие задачи на движение

Пример №1:

Из пункта А в пункт В выехал автомобиль. Одновременно с ним выехал другой автомобиль, который ровно половину пути ехал со скоростью на   км/ч меньшей, чем первый, а вторую половину пути он проехал со скоростью   км/ч.

В результате автомобили прибыли в пункт В одновременно.

Найдите скорость первого автомобиля, если известно, что она больше   км/ч.

Решение №1:

Слева от знака равно запишем время первого автомобиля, а справа – второго:

 .

Упростим выражение в правой части:

 .

Поделим каждое слагаемое на АВ:

 .

Получилось обычное рациональное уравнение. Решив его, получим два корня:

 

Из них только один больше  .

Ответ:   км/ч.

Если тебе непонятно, как получились эти корни, прочитай тему «Рациональные уравнения».

 

Пример №2

Из пункта A круговой трассы выехал велосипедист. Через   минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через   минут после отправления он догнал велосипедиста в первый раз, а еще через   минут после этого догнал его во второй раз. Найдите скорость велосипедиста, если длина трассы равна   км. Ответ дайте в км/ч.

Решение:

Здесь будем приравнивать расстояние.

Пусть скорость велосипедиста будет  , а мотоциклиста –  . До момента первой встречи велосипедист был в пути   минут, а мотоциклист –  .

При этом они проехали равные расстояния:

 

Между встречами велосипедист проехал расстояние  , а мотоциклист –  . Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:

Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили– спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.

Значит,

 

Полученные уравнения решаем в системе:

 

Ответ:  .

КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

1. Основная формула

 , или  

2. Относительное движение

• Это сумма скоростей, если тела движутся навстречу друг другу;
• разность скоростей, если тела движутся в одном направлении.

3. Движение с течением:

• Если движемся по течению, к нашей скорости прибавляется скорость течения;
• если движемся против течения, из скорости вычитается скорость течения.

Мы помогли тебе разобраться с задачами на движение…

Теперь твой ход…

Если ты внимательно прочитал текст и прорешал самостоятельно все примеры, готовы спорить, что ты все понял. 

И это уже половина пути.

Напиши внизу в комментариях разобрался ли ты с задачами на движение?

Какие вызывают наибольшие трудности?

Понимаешь ли ты, что задачи на «работу» — это почти тоже самое? 

Напиши нам и удачи на экзаменах!

 

 

 

А также получить доступ к учебнику YouClever без ограничений…

12 хитростей для начинающих водителей, о которых не рассказывают в автошколе

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Даже те, кто не первый день за рулем, не всегда знают о тонкостях и нюансах, которые облегчают водительскую жизнь.

AdMe.ru рассказывает, как почувствовать себя на дороге в своей тарелке, научиться избегать опасных ситуаций и стать уверенным водителем.

12. Проверьте, правильно ли настроены зеркала

Если зеркала настроены неверно, то возникает слепая зона — часть дороги, которую вы не видите, поэтому можете не заметить автомобиль на соседней полосе. Чтобы ее не было, настройте боковые зеркала так, чтобы ваша машина не была в них видна (либо была видна совсем чуть-чуть). Чтобы проверить, нет ли слепой зоны, медленно двигайтесь задним ходом мимо другой стоящей машины, глядя в боковое зеркало. Как только она исчезла из зеркала, вы должны увидеть ее боковым зрением. Зеркало заднего вида настраивается так, чтобы в нем было полностью видно заднее стекло автомобиля. Когда настраиваете зеркала, примите ту позу, в которой обычно водите машину.

11. Научитесь чувствовать, где находятся колеса

Чтобы уметь объезжать ямы на дороге и не царапать диски при парковке у бордюра, нужно научиться чувствовать, где находятся колеса автомобиля. Для этого возьмите пустую пластиковую бутылку, сомните ногой и положите на асфальт. Потренируйтесь наезжать на ее по очереди правым и левым передним колесом. Откройте окно, чтобы слышать хруст бутылки.

10. Паркуйтесь, ориентируясь на окна и зеркала

Если вы паркуетесь передом к бордюру, останавливайтесь, как только увидите бордюр под боковым зеркалом. Так расстояние до бордюра будет минимальным, а вы не поцарапаете бампер.

Если вы паркуетесь передом параллельно бордюру, нужно позаботиться о том, чтобы не поцарапать диски. Наклейте кусочек цветного скотча внизу лобового стекла. Как только линия бордюра совпадет с меткой, останавливайтесь. Лучше парковаться параллельно бордюру задом — тогда бордюр виден в боковых зеркалах и вы не прижметесь к нему вплотную.

Как и почему движется автомобиль?

Откуда возникает движущая сила, если автомобиль не толкают как тележку и его не тянет лошадь? Почему он едет? Что такое избыточная мощность? Как ни странно, на эти вопросы не всякий может ответить. Между тем, вопрос этот весьма прост, и разобраться в нем по силам даже школьнику

Многие из нас встречали картинку: улица прошлого века, и на мостовой — экипаж без лошадей. Такими примерно были «самобеглые коляски» русских изобретателей Шамшуренкова и Кулибина. Катил «самобеглую» стоявший на педалях человек. Его «механическая энергия » передавалась на ведущие колеса, которые и толкали коляску. Этот же принцип лег в основу другого «самодвижущегося экипажа», появившегося позднее, — автомобиля. Только источником механической энергии у него стал двигатель внутреннего сгорания. Как же его энергия приводит в движение автомобиль?

Где толкающая сила?

Рычаг-помощник

Откуда же она возникает, если автомобиль не толкают как тележку и его не тянет лошадь?
Чтобы ответить на этот вопрос, давайте разберем способ, которым можно тележку передвигать, — при помощи рычага. А чтобы нижний конец его не скользил, — забьем в землю клин.
Первый вариант — толкаем рычагом непосредственно тележку. Она сдвинется и в том случае, когда рычаг воздействует прямо на ось колеса, причем плечо, на которое действует рука, получается вдвое большим. Эту работу можно облегчить — придавить рычаг с такой силой, чтобы, опираясь на дорогу, его нижний конец не проскальзывал. Останется лишь непрерывно переставлять его.
А если прилагать силу к верхней части колеса по касательной к окружности? Тогда полоску, выделенную на рисунке посредине пунктиром, можно рассматривать как такой же рычаг, бес машины прижимает ведущее колесо к дороге — оно не пробуксовывает, значит, нижний конец нашего «рычага» как бы удерживается колышком и ось колеса переместится под действием силы F.
Когда ось продвинется несколько вперед — колесо провернется и «конец рычага» — точка 1 уже не будет соприкасаться с дорогой. Ее место займет точка 2, затем точка 3 и так далее.
Таким образом, колесо можно рассматривать как бы состоящим из бесконечного числа рычагов, непрерывно и последовательно сменяющих один другой. Оно удобнее рычага — ничего не нужно переставлять. Способ перекатывания повозки за обод колеса применяют, когда надо помочь лошади. Подобным образом поступают и артиллеристы, выкатывая вручную орудия на огневые позиции: это легче, ибо усилие на оси получается вдвое большим, чем в том случае, если толкать за станину.
Однако лучше не толкать и не тянуть колесо, а вращать. Так нельзя ли найти такой способ, чтобы не толкать и не тянуть колесо, перехватывая его все время за обод? Можно. Для этого достаточно передавать на колесо через ось вращающее усилие, или, как принято говорить в технике, подвести к нему крутящий момент. Крутящий момент стремится провернуть колесо, но этому препятствует сила трения, возникающая между ним и дорогой. Колесо как бы отталкивается от земли и начинает катиться. Здесь главный помощник — трение, без него движение невозможно. Известно, как беспомощен автомобиль, например, на льду.

Разные дороги и разные силы

Всё — «против»

По асфальту тележка катится легко. Но вот колеса попали на мягкий грунт или песок. Толкать ее,стало труднее. B чем дело? Возросла сила, которую в теории автомобиля называют силой сопротивления качению.
А если встретится подъем? Добавляется сила, стремящаяся скатить тележку.
А встречный ветер? Каждый из нас знает, как трудно двигаться, когда он сильный. Но мчащийся автомобиль сам ‘«устраивает» себе искусственный встречный ветер, и тем сильнее, чем больше скорость.
Кроме того, при разгоне тележку приходится толкать намного сильнее, чем при. равномерном движении: нужно преодолевать силы инерции.
Итак, автомобиль равномерно движется по хорошей горизонтальной дороге: нужна умеренная толкающая сила — лишь для того, чтобы преодолевать трение и сопротивление воздуха.
Но ведь сначала надо тронуться с места. А для этого требуется самая большая толкающая сила. Хотим ускорить движение — надо преодолеть инерцию, опять, же необходимо увеличение толкающей силы. Съехали на плохую дорогу или поднимаемся в гору. И здесь толкающая сила должна намного возрасти. Обычно в зависимости от условий движения она меняется в несколько раз. Соответственно должен меняться и подводимый к колесам крутящий момент. Мы видим: чтобы автомобиль мог двигаться по различным дорогам и с разной скоростью, надо иметь возможность увеличивать и уменьшать крутящий момент на его колесах в широких пределах.

Упрямый характер

От двигателя — и колесам

Скорость вращения коленчатого вала двигателя внутреннего сгорания может изменяться примерно от пятисот, когда он работает на «холостом ходу», до нескольких тысяч оборотов в минуту. Казалось бы, можно двигаться с различной скоростью, даже если мотор непосредственно соединить с колесами: быстрее вращается вал двигателя — и, пожалуйста, с большей скоростью идет машина.

У бензинового «характер» хуже

Но вот дорога пошла в гору, и сразу автомобильный двигатель показывает свой «характер». Он значительно снижает обороты (труднее стало тянуть), но крутящий момент увеличивается недостаточно: на десять процентов, на тридцать, самое большое — на пятьдесят. У дизельных двигателей такая «приспособляемость» еще хуже. Давайте взглянем на график. Он показывает, как меняется величина крутящего момента бензинового автомобильного двигателя. Видно и самое худшее: с какого-то числа оборотов (в этом месте поставлена галочка) крутящий момент непрерывно уменьшается.
Действительно, при снижении числа оборотов с 4500 до 3000 крутящий момент возрос с 7 до 9 кгм. Но если подъем, допустим, потребовал большего, двигатель внутреннего сгорания не может справиться с этой задачей: необходимо увеличение момента, а он начинает уменьшаться, скорость движения резко падает — обороты двигателя идут на убыль… крутящий момент становится еще меньше…
В том же диапазоне чисел оборотов современного тягового электродвигателя крутящий момент увеличивается примерно в четыре раза.
В этом отношении для автомобиля больше подошли бы двигатели паровые или электромоторы, как бы отвечающие золотому правилу механики: при большой нагрузке они сбавляют обороты, а тянут сильнее. Но двигатель плюс котельная установка слишком громоздки для автомобиля, а возить на нем электростанцию просто невозможно. Двигатель же внутреннего сгорания обладает пока многими другими преимуществами. А на его «дурной характер» можно найти управу.

 

Выход есть!

Можно и быстро и медленно

 Силы человека, работавшего на педалях «самобеглой» коляски, хватало на движение по ровной дороге. А на подъеме? Для его преодоления между «двигателем» и ведущими колесами был помещен специальный зубчатый барабан. Он позволял увеличить крутящий момент, подводимый к колесам, за счет скорости их вращения, — а следовательно, и скорости движения коляски. Крутящий момент увеличивался, когда ведущая шестерня соединялась с рядом зубьев барабана, расположенных дальше от оси (наибольшее плечо) и, наоборот, — уменьшался при укорочении плеча.
Так же меняется величина крутящего момента и в шестеренчатой передаче, распространенной в современной технике.

Это делает Коробка передач

И вперед и назад

Менять величину крутящего момента двигателя может механизм, в котором будет несколько пар зацепленных одна с другой шестерен, — допустим, три — с различными передаточными числами: 1:4; 1:2 и 1:1. Первые два позволяют увеличить крутящий момент (толкающую силу) в четыре или в два раза.
Схема такого механизма — коробки передач — показана на рисунке. В общем корпусе находятся три пары шестерен с разными передаточными числами. Шестерни ведомого вала, через который вращение передается к колесам, могут передвигаться вдоль него, все время вращаясь с ним. Действуя рычагом переключения, водитель может соединить любую пару и двигаться на любой из трех передач. Это первая услуга коробки.
Вторая услуга. На рисунке коробка показана в положении «включена первая передача». Если расцепить и эту пару — вращение от двигателя к колесам передаваться не будет. Такое положение называется нейтральным.
При нейтральном положении двигатель не соединен с колесами, и поэтому его легко пустить, прогреть, не надо выключать при остановке перед светофором и т. п.
Третья услуга. Даже мотоцикл случается подать назад. Автомобилю — это просто необходимо. Надо и развернуться и встать под погрузку, подъехать к прицепу…
В общем, ведущие колеса должны вращаться и назад. А двигатель? Его коленчатый вал вращается только в одну сторону. Значит, коробка должна иметь передачу заднего хода. Между ведущим и ведомым валами в зацепление вводится «лишняя» шестерня или две на общей оси, как показано на рисунке. Она и меняет направление вращения ведомого вала.

Чтобы трогаться плавно

Просто соединить шестерни первой передачи не удастся — одна вращается, другая неподвижна. А если включить передачу принудительно — машина «прыгнет» вперед или заглохнет двигатель, да и для зубьев шестерен это небезопасно.
Избавиться от таких неприятностей и плавно тронуться с места позволяет особый механизм — «сцепление», которое располагают между двигателем и коробкой. Оно имеет два положения: сцепление включено — крутящий момент передается на коробку; сцепление выключено — она отсоединена от двигателя.
Для передачи вращения здесь используется сила трения между маховиком и ведомым диском. Расположенные по окружности пружины прижимают диск к маховику, и он вращается вместе с ним — сцепление включено. В таком положении оно находится при движении автомобиля. Пружины обеспечивают такую силу трения, которая необходима для передачи крутящего момента двигателя, без пробуксовки между маховиком и ведомым диском.
Когда водитель нажмет ногой на левую педаль (так принято на автомобилях всего мира), диск, преодолевая усилие пружин, отходит от маховика. Мы говорим: сцепление выключено. Передача крутящего момента от двигателя прекращается, хотя его коленчатый вал и маховик продолжают вращаться.
В таком положении — педаль нажата — водитель включает передачу и, плавно отпуская педаль, постепенно приближает ведомый диск к гладкой поверхности маховика. В это время общая сила давления пружин все увеличивается и сила трения возрастает. Маховик постепенно, плавно увлекает диск, который со все уменьшающимся проскальзыванием начинает вращаться, и… машина плавно трогается. Успех этого процесса зависит от искусства водителя, поначалу частенько он проходит не совсем гладко.
Когда нужно переключить передачу — «перейти», например, при разгоне с первой на вторую или со второй на третью — водитель каждый раз нажимает на педаль сцепления.

Ну а теперь самое главное. Эту статью написал кандидат технических наук В. Гусев, еще в 1968 году…  Как оказывается, по большому счету в автомобиле мало что изменилось с тех пор. Те же шестерни, коробки, рычаги. И все тот же ДВС, пусть и усовершенствованный. Качественного скачка, какой был при переходе от лошади к автомобилю, или при изобретении самолета, нет.

Вопросы из экзаменационных билетов ГАИ (ГИБДД)

Украина

Примечание:   Правильный ответ   Неправильный ответ

1. Какой автомобиль более устойчив к опрокидыванию?

1 Гружёный грузовой автомобиль.

2 Незагруженный грузовой автомобиль.

К опрокидыванию более устойчив незагруженный грузовой автомобиль. Это объясняется тем, что устойчивость автомобиля в повороте будет больше, если его центр тяжести будет ниже. А центр тяжести незагруженного автомобиля всегда расположен ниже, чем у груженого.

2. Как пользоваться тормозами на покрытой листьями, скользкой дороге?

1 Выключить сцепление и плавно тормозить.

2 Тормозить плавно, прерывистыми нажатиями на педаль тормоза, не выключая сцепления и не производя резких поворотов рулевого колеса.

На дороге, где возможно скольжение автомобиля, тормозите плавно, прерывистыми нажатиями на педаль тормоза, не выключая сцепления и не производя резких поворотов рулевого колеса.

3. Уменьшение тормозного пути на скользкой дороге для заднеприводного автомобиля достигается:

1 Прерывистым торможением с выключенным сцеплением.

2 Прерывистым торможением без выключения сцепления и передачи.

4. В каком случае центробежная сила при повороте уменьшается?

1 При уменьшении радиуса поворота.

2 При резком повороте рулевого колеса в сторону поворота.

3 При снижении скорости движения.

При снижении скорости движения центробежная сила при повороте уменьшится.

5. Двигаясь со скоростью около 60 км/ч, Вы внезапно попали на небольшой участок дороги с гололедицей. Что следует предпринять в данной ситуации?

1 Не меняя положения рулевого колеса, выключить передачу и двигаться накатом.

2 Не меняя положения рулевого колеса и скорости движения, проехать скользкий участок дороги.

Скользкий участок дороги следует проехать, не меняя положения рулевого колеса и скорости движения.

6. Для обеспечения безопасности движения после преодоления глубоких луж водителю рекомендуется:

1 На короткой дистанции пробега несколькими нажатиями на тормозную педаль просушить тормозные накладки.

2 Двигаться с ускорением на более высоких передачах.

После преодоления глубоких луж водителю рекомендуется просушить тормозные накладки, выполнив несколько нажатий на тормозную педаль на короткой дистанции пробега.

7. По дороге движется автомобиль, водитель которого включил указатель поворота налево и длительное время его не выключает. Как должен поступить водитель, движущийся за ним?

1 Обогнать движущийся впереди автомобиль.

2 Не изменять режим своего движения.

3 Не обгонять движущийся впереди автомобиль. При наличии безопасной возможности — опередить его с правой стороны.

Если вы видите, что на автомобиле, едущем перед вами, долго горит левый указатель поворота, ни в коем случае не обгоняйте этот автомобиль. Возможно, его водитель сигнализирует вам о наличии опасности на встречной полосе. Можете осуществить опережение впередиидущего автомобиля с правой стороны, если это будет безопасно.

8. При движении на косогорах водитель должен:

1 Вести автомобиль с ускорением, поворачивая рулевое колесо в сторону, противоположную уклону, а при сползании автомобиля – в сторону уклона.

2 Вести автомобиль медленно, избегая резких поворотов рулевым колесом.

На косогорах водитель должен ехать с низкой скоростью, не применяя резких поворотов рулевым колесом.

9. Как следует поступить, если во время движения произошел прокол шины колеса?

1 Резко затормозить и остановиться.

2 Крепко держать рулевое колесо и плавно остановиться.

3 Повернуть рулевое колесо в сторону повреждённой шины и затормозить.

Если вы почувствовали, что произошел прокол шины колеса, крепко удерживая рулевое колесо, плавно остановитесь.

10. Что необходимо сделать водителю в случае внезапного разрыва шины при движении автомобиля?

1 Удерживая рулевое колесо, сохранить прямолинейное движение, снизить скорость и остановиться.

2 Резко затормозить рабочим тормозом до полной остановки.

3 Остановить автомобиль при помощи стояночного тормоза.

Если при движении автомобиля произошел внезапный разрыв шины, водителю следует, сохранить прямолинейное движение, крепко удерживая рулевое колесо, снизить скорость и остановиться.

11. Какой из перечисленных приёмов торможения на скользком участке дороги наиболее эффективен и безопасен?

1 Выключить сцепление и нажать на педаль тормоза.

2 Периодически нажимать на педаль тормоза, не выключая сцепления.

3 Нажать на педаль тормоза и не выключать сцепление.

На скользком участке дороги эффективнее и безопаснее всего тормозить, периодически нажимая на педаль тормоза, не выключая сцепления.

12. При движении в условиях тумана расстояние до предметов представляется:

1 Менее отдалённым, чем в действительности.

2 Более отдалённым, чем в действительности.

3 Соответствующим действительному.

В тумане расстояние до предметов кажется больше, чем есть на самом деле.

13. Для предотвращения опасных последствий заноса автомобиля водитель должен:

1 Прекратить начатое торможение.

2 Резко нажать на педаль тормоза.

3 Нажать на педаль сцепления.

При возникновении заноса автомобиля, необходимо прекратить начатое торможение во избежание непоправимых последствий.

14. В каком из перечисленных случаев водителю можно убрать одну руку с рулевого колеса во время движения?

1 Только для включения одного из рычагов органов управления транспортным средством.

2 Только во время курения.

3 В случаях, указанных в ответах 1 и 2.

Водитель может убрать руку с рулевого колеса только в случае необходимости включения одного из рычагов управления в автомобиле.

15. К чему приводит пониженное давление воздуха в шинах передних колес автомобиля?

1 К затруднению управления автомобилем.

2 К увеличению тормозного пути.

3 К увеличению скорости движения.

При пониженном давлении воздуха в шинах передних колес управление автомобилем затруднено.

16. Как влияет утомление на внимание и реакцию водителя?

1 Внимание и реакция водителя снижаются.

2 Внимание и реакция водителя повышаются.

3 Не влияет на внимание и реакцию водителя.

При утомлении водитель медленнее реагирует на ситуацию, его внимание и способность к концентрации снижаются.

17. Вы остановились на подъёме в ожидании разрешающего сигнала светофора. При этом удерживать автомобиль на месте лучше всего:

1 За счет пробуксовки сцепления при включённой первой передаче.

2 Выключенным двигателем с установленной пониженной передачей.

3 Рабочим тормозом.

4 Стояночным тормозом.

18. Применение торможения двигателем на скользкой дороге для заднеприводного автомобиля:

1 Снижает устойчивость автомобиля.

2 Повышает устойчивость автомобиля.

3 Не оказывает какого-либо влияния на устойчивость автомобиля.

19. Что рекомендуется предпринять водителю, если при движении в тёмное время суток встречное транспортное средство в какой-то мере ослепляет его?

1 Прищурить глаза.

2 Переводить взгляд периодически то влево, то вправо.

3 Переводить взгляд периодически вправо, ориентируясь на белую линию дорожной разметки, обозначающую край проезжей части.

Если при движении в тёмное время суток встречное транспортное средство частично ослепляет водителя, рекомендуется периодически переводить взгляд вправо, не выпуская из виду белую линию дорожной разметки, которой обозначен край проезжей части.

20. Резкое торможение транспортного средства при интенсивном движении:

1 Сказывается только на техническом состоянии автомобиля.

2 Является обычным приемом управления при интенсивном движении.

3 Может способствовать наезду сзади.

Если вы резко затормозите, то велика вероятность, что водитель транспортного средства, ехавшего за вами, не успеет вовремя сориентироваться и наедет на вас. Не допускайте резких торможений!

21. С какой стороны разрешается водителю сесть в автомобиль?

1 Только с той стороны автомобиля, которая ближе к тротуару.

2 Только с левой стороны.

3 Только с правой стороны.

4 Со стороны расположения руля, не создавая препятствий другим участникам дорожного движения.

Водитель может сесть в автомобиль со стороны расположения руля, если при этом он не создаст препятствий другим участникам дорожного движения.

22. В каком случае увеличивается центробежная сила, действующая на автомобиль на поворотах дороги?

1 С увеличением скорости движения.

2 С уменьшением скорости движения.

3 С увеличением радиуса поворота.

Центробежная сила, возникающая при поворотах, будет тем больше, чем больше скорость движения.

23. Водитель движется по дороге с двусторонним движением, соблюдая соответствующую дистанцию. Его начинает обгонять другое транспортное средство, и внезапно появляется встречное. Как должен поступить водитель обгоняемого транспортного средства?

1 Освободить занимаемую полосу движения, снизив свою скорость.

2 Освободить занимаемую полосу движения, увеличив свою скорость.

3 Подать звуковой сигнал и продолжить движение, не изменяя скоростной режим.

Водитель должен освободить занимаемую полосу движения, снизив скорость, чтобы дать возможность обгонявшему транспортному средству вернуться на свою полосу для движения.

24. Вы выехали для обгона и неожиданно увидели встречный автомобиль. Если Вы не уверены в том, что сумеете завершить обгон, Вы должны:

1 Снизить скорость и вернуться на ранее занимаемую полосу.

2 Слегка увеличить скорость и быстрее завершить обгон, подавая звуковой сигнал и включив фары.

Если у вас нет уверенности в том, что вы успеете завершить обгон и избежать столкновения со встречным транспортным средством, тогда вы должны снизить скорость и вернуться на ранее занимаемую полосу.

25. Для безопасности дорожного движения в условиях сильного тумана водителю рекомендуется:

1 Включить задние противотуманные фонари и сократить дистанцию, чтобы ориентироваться по габаритным фонарям впереди движущегося транспортного средства.

2 Включить задние противотуманные фонари и увеличить дистанцию движения.

3 Рекомендуется любое из указанных в ответах 1 и 2 действий.

В условиях сильного тумана и, как следствие, плохой видимости, водителю рекомендуется включить задние противотуманные фонари и увеличить дистанцию движения, чтобы транспортное средство было хорошо заметно другим транспортным средствам и была возможность безопасных маневров.

26. С какой безопасной скоростью следует выполнить поворот на пересекаемую дорогу?

1 Снизить скорость при въезде в поворот и увеличить её при выезде из поворота.

2 Двигаться, не снижая скорости движения, но соблюдая особую осторожность.

3 Снизить скорость движения лишь в том случае, если дорога скользкая.

27. При движении на повороте автомобиль более устойчив, если движение осуществляется:

1 С увеличением скорости.

2 С выключенной передачей.

3 С включённой передачей.

При движении с включенной передачей автомобиль более устойчив при повороте.

28. Двигаясь прямо, вы внезапно попали на скользкий участок дороги. Что следует предпринять в данной ситуации?

1 Не меняя положения рулевого колеса, выключить передачу и двигаться накатом.

2 Не меняя положения рулевого колеса и скорости движения, проехать скользкий участок дороги.

3 Не меняя положения рулевого колеса, увеличить скорость движения автомобиля на данном участке.

4 Проехать скользкий участок дороги, не меняя положения рулевого колеса, притормаживая, не выключая сцепления.

Скользкий участок на дороге следует проехать, не меняя положения рулевого колеса и скорости движения.

29. Во сколько раз увеличивается тормозной путь при увеличении скорости в два раза?

1 Величина тормозного пути не зависит от скорости движения.

2 В два раза.

3 В три раза.

4 В четыре раза.

Тормозной путь увеличивается в четыре раза при увеличении скорости всего лишь в два раза.

30. Как рекомендуется двигаться по участку дороги, который залит водой?

1 Перед въездом на участок ускорить движение и не снижать скорости до выезда с него.

2 Перед въездом на участок снизить скорость движения и проехать его не ускоряясь.

3 Перед въездом на участок снизить скорость движения, а на самом участке увеличить её.

Перед въездом на участок дороги, который залит водой, необходимо снизить скорость движения и проехать его без ускорения.

31. Какую передачу рекомендуется включить при стоянке на подъёмах, чтобы не допустить самопроизвольного движения транспортного средства?

1 Передачу для движения назад вместе со стояночным тормозом.

2 Первую передачу вместе со стояночным тормозом.

3 Нейтральную передачу вместе со стояночным тормозом.

Останавливаясь на подъемах, чтобы не допустить самопроизвольного движения автомобиля, необходимо включить первую передачу вместе со стояночным тормозом.

32. Как пользоваться тормозами на скользкой дороге?

1 Тормозить резкими, прерывистыми нажатиями на педаль тормоза.

2 Выключить сцепление и плавно тормозить.

3 Плавно тормозить, не выключая сцепления, и резко не поворачивать рулевое колесо.

На скользком участке дороги следует тормозить плавно, не выключая сцепления. Недопустимо при этом резко поворачивать рулевое колесо.

33. В дождливую погоду следует соблюдать дистанцию:

1 Больше обычной.

2 Меньше обычной.

3 Обычную, но вести транспортное средство следует с повышенным вниманием.

В дождливую погоду следует придерживаться дистанции, которая будет больше обычной. Эта рекомендация связана с тем, что на мокром покрытии увеличивается тормозной путь автомобиля.

34. Что должен сделать водитель, если он увидел животное, внезапно появившееся на проезжей части?

1 Включить звуковой сигнал.

2 Постараться побыстрее объехать животное, подавая короткие прерывистые звуковые сигналы.

3 Снизить скорость, а в случае необходимости – остановиться.

При возникновении опасности для движения или препятствия, которое водитель способен объективно обнаружить, он должен немедленно принять меры к снижению скорости, вплоть до остановки транспортного средства либо безопасного объезда препятствия.

35. В чем опасность длительного торможения автомобиля с выключенной передачей на крутых затяжных спусках?

1 Повышенный износ деталей сцепления.

2 Перегрев тормозных механизмов и отказ их в работе.

3 Повышенный износ шин.

При длительном торможении с выключенной передачей на затяжных спусках велика вероятность того, что произойдет перегрев тормозных механизмов и их отказ в работе.
Примечание.
Крутой спуск обозначается предупреждающим дорожным знаком «Крутой спуск» (с противоположной стороны устанавливается дорожный знак «Крутой подъём»). На обозначенных участках дорог запрещается движение с неработающим двигателем и выключенными сцеплением или передачей, буксировка на гибкой сцепке, любая буксировка в гололед.

36. Скорость движения на таком повороте оказалась большой. Как должен поступить водитель в целях безопасности дорожного движения?

1 Снизить скорость движения и при необходимости притормозить.

2 Не снижая скорости, выехать на полосу встречного движения, если она свободна от других транспортных средств.

3 Выполняя неотложное служебное задание, разрешается выехать на полосу встречного движения, не снижая скорость.

Россия

Примечание:   Правильный ответ   Неправильный ответ

1. В какой момент следует начинать отпускать стояночный тормоз при трогании на подъеме?

1 До начала движения.

2 После начала движения.

3 Одновременно с началом движения.

При трогании на подъеме стояночный тормоз следует начинать отпускать одновременно с началом движения. Если его отпустить до начала движения, то может произойти скатывание автомобиля. Если же отпустить тормоз после начала движения, то произойдет остановка двигателя.

2. Что следует сделать водителю, чтобы предотвратить возникновение заноса при проезде крутого поворота?

1 Перед поворотом снизить скорость и выжать педаль сцепления, чтобы дать возможность автомобилю двигаться накатом на повороте.

2 Перед поворотом снизить скорость, при необходимости включить пониженную передачу, а при проезде поворота не увеличивать резко скорость и не тормозить.

3 Допускается любое из перечисленных действий.

Для предотвращения возможного заноса водитель должен перед поворотом заблаговременно снизить скорость и при необходимости включить пониженную передачу, не прибегая к резкому увеличению скорости и торможению.
Занос автомобиля при проезде крутого поворота возникает под действием центробежной силы. Чем выше скорость, тем больше эта сила. Поэтому прохождение поворота с выключенным сцеплением может привести к потере контроля над управлением.

3. В каком случае легковой автомобиль более устойчив против опрокидывания на повороте?

1 Без груза и пассажиров.

2 С пассажирами, но без груза.

3 Без пассажиров, но с грузом на верхнем багажнике.

Более устойчив к опрокидыванию при повороте ненагруженный автомобиль, поскольку опрокидывающий момент зависит от высоты расположения центра тяжести. У ненагруженного автомобиля центр тяжести расположен ниже, чем у нагруженного, следовательно опрокидывающий момент у него меньше.

4. Считаете ли Вы безопасным движение на легковом автомобиле в темное время суток с ближним светом фар по неосвещенной загородной дороге со скоростью 90 км/ч?

1 Да, так как предельная допустимая скорость соответствует требованиям Правил.

2 Нет, так как остановочный путь превышает расстояние видимости.

Остановочный путь автомобиля со скорости 90 км/ч будет равен примерно 90-100 м. Ближний свет фар обеспечивает видимость в пределах 30-40 м впереди автомобиля. Следовательно, движение на скорости 90 км/ч по неосвещенной дороге является небезопасным, поскольку остановочный путь значительно больше расстояния видимости. Если вы и заметите препятствие на пути, то не успеете затормозить.

5. Что подразумевается под остановочным путем?

1 Расстояние, пройденное транспортным средством с момента обнаружения водителем опасности до полной остановки.

2 Расстояние, пройденное транспортным средством с момента начала срабатывания тормозного привода до полной остановки.

3 Расстояние, соответствующее тормозному пути, определенному технической характеристикой данного транспортного средства.

Под остановочным путем подразумевается расстояние, пройденное ТС с момента обнаружения водителем опасности до полной остановки. Это расстояние во многом зависит от скорости реакции водителя и времени срабатывания тормозного привода.
Остановочный путь всегда больше тормозного. При усталости водителя его скорость реакции снижается, следовательно и на тормоз он нажмет с опозданием.

6. При движении в условиях тумана расстояние до предметов представляется:

1 Большим, чем в действительности.

2 Меньшим, чем в действительности.

3 Соответствующим действительности.

При движении в условиях тумана водитель должен учитывать, что расстояние до предметов кажется больше, чем есть на самом деле.

7. Чем опасно длительное торможение с выключенным сцеплением (передачей) на крутом спуске?

1 Значительно увеличивается износ протектора шин.

2 Повышается износ деталей тормозных механизмов.

3 Перегреваются тормозные механизмы и уменьшается эффективность торможения.

При длительном торможении с выключенной передачей на затяжных спусках велика вероятность того, что произойдет перегрев тормозных механизмов и снизится эффективность торможения.

8. На каком рисунке показано правильное положение рук на рулевом колесе?

1 На левом.

2 На среднем.

3 На правом.

Правильное положение рук показано на правом рисунке. При таком положении рук у водителя есть возможность выполнить любой маневр, не потеряв при этом контакта с рулевым колесом.

9. Как должен поступить водитель в случае потери сцепления колес с дорогой изза образования «водяного клина»?

1 Увеличить скорость.

2 Снизить скорость резким нажатием на педаль тормоза.

3 Снизить скорость, применяя торможение двигателем.

«Водяной клин» может образоваться во время сильного дождя в зоне контакта колес с покрытием. Особенно велика вероятность его образования при изношенном протекторе шин. При потере сцепления колес с дорогой из-за образования «водяного клина» водитель должен плавно снизить скорость, применяя торможение двигателем. Следует помнить, что любое резкое изменение скорости может привести к заносу авто.

10. При движении по какому участку дороги действие сильного бокового ветра наиболее опасно?

1 По открытому.

2 По закрытому деревьями.

3 При выезде с закрытого участка на открытый.

Наиболее опасным действие сильного бокового ветра будет при выезде с закрытого участка на открытый. Возникающий при этом сильный порыв ветра может повлиять на курсовую устойчивость автомобиля.

11. Зависит ли выбор бокового интервала от скорости движения?

1 Выбор бокового интервала от скорости движения не зависит.

2 При увеличении скорости движения боковой интервал необходимо увеличить.

Изменение скорости в силу различных внешних и внутренних факторов (боковая эластичность колес, неровности покрытия, люфт рулевого механизма) влияет на поперечные отклонения от заданной траектории движения. Поэтому с увеличением скорости необходимо увеличивать и боковой интервал.

12. В темное время суток и в пасмурную погоду скорость встречного автомобиля воспринимается:

1 Ниже, чем в действительности.

2 Выше, чем в действительности.

3 Восприятие скорости не меняется.

В темное время суток и в пасмурную погоду скорость встречного автомобиля кажется ниже, чем есть на самом деле. Будьте осторожны при встречном разъезде, обгоне и объезде.

13. Для прекращения заноса, вызванного торможением, водитель в первую очередь должен:

1 Прекратить начатое торможение.

2 Выключить сцепление.

3 Продолжить торможение, не изменяя усилия на педаль тормоза.

Занос на скользком участке дороги может быть вызван блокировкой задних колес автомобиля при торможении. В первую очередь необходимо прекратить начатое торможение. Затем поворотом руля в сторону заноса можно выровнять траекторию движения.

14. Принято считать, что среднее время реакции водителя составляет:

1 Примерно 0,5 секунды.

2 Примерно 1 секунду.

3 Примерно 2 секунды.

Время реакции водителя зависит от его психофизических особенностей, опыта, дорожной обстановки, степени усталости, эмоционального состояния и многих других факторов. Считается, что водитель среагирует на ситуацию за время примерно от 0,4 до 1,6 секунды. Поэтому принято считать, что среднее время реакции водителя составляет около 1,0 секунды.

15. Как следует поступить водителю, если во время движения по сухой дороге с асфальтобетонным покрытием начал моросить дождь?

1 Уменьшить скорость и быть особенно осторожным.

2 Не изменяя скорости продолжить движение.

3 Увеличить скорость и попытаться проехать как можно большее расстояние, пока не начался сильный дождь.

С первыми каплями дождя водитель должен снизить скорость и двигаться более осторожно, поскольку на мокром асфальтобетонном покрытии тормозной путь значительно увеличивается и в случае обнаружения опасности быстро остановиться не удастся.

16. Как изменяется длина тормозного пути легкового автомобиля при движении с прицепом, не имеющим тормозной системы?

1 Уменьшается, так как прицеп оказывает дополнительное сопротивление движению.

2 Увеличивается.

3 Не изменяется.

При движении с прицепом, не имеющим своей тормозной системы, тормозной путь автомобиля увеличится, поскольку увеличится масса транспортного средства.

17. Какой стиль вождения обеспечит наименьший расход топлива?

1 Частое и резкое ускорение при плавном замедлении.

2 Плавное ускорение при резком замедлении.

3 Плавное ускорение при плавном замедлении.

Наименьший расход топлива обеспечит плавное ускорение при плавном замедлении.

18. При движении в плотном потоке Вы заметили сзади транспортное средство, движущееся на слишком малой дистанции. Как следует поступить, чтобы обеспечить безопасность движения?

1 Увеличить скорость движения, уменьшив дистанцию до движущегося впереди транспортного средства.

2 Предупредить следующего сзади водителя резким кратковременным торможением.

3 Скорректировать скорость движения, ослабив нажатие на педаль газа, чтобы увеличить дистанцию до движущегося впереди транспортного средства.

4 Допускается любое из перечисленных действий.

В описанной ситуации целесообразнее всего ослабить нажатие на педаль газа. Тем самым увеличится дистанция до движущегося впереди транспортного средства. Таким образом появится дополнительное пространство для интенсивного торможения в случае необходимости. Резко тормозить в такой ситуации нельзя, поскольку это может привести к наезду сзади.

19. Какое расстояние проедет транспортное средство за одну секунду при скорости движения около 90 км/час?

1 Примерно 15 м.

2 Примерно 25 м.

3 Примерно 35 м.

Чтобы рассчитать, какое расстояние проезжает транспортное средство на такой скорости, нужно перевести часы в секунды: 1 час = 3600 сек. Разделим теперь 90 км на 3600 сек. S = 90/3600 = 0,025 км, что равняется 25 метрам.

20. Как изменяется поле зрения водителя с увеличением скорости движения?

1 Не изменяется.

2 Расширяется.

3 Сужается.

С увеличением скорости водитель должен смотреть намного дальше впереди автомобиля, чтобы успеть оценить ситуацию, поэтому поле зрения водителя сужается.

21. При торможении двигателем на крутом спуске водитель должен выбирать передачу, исходя из условий:

1 Чем круче спуск, тем выше передача.

2 Чем круче спуск, тем ниже передача.

3 Выбор передачи не зависит от крутизны спуска.

Более низкая передача на крутом спуске обеспечит лучшую эффективность торможения двигателем, поэтому выбирать передачу следует, исходя из условия: чем круче спуск, тем ниже передача.

22. Что должен сделать водитель, чтобы быстро восстановить эффективность тормозов после проезда через водную преграду?

1 Продолжить движение, немного натянув рычаг ручного тормоза.

2 Продолжить движение и просушить тормозные колодки многократными непродолжительными нажатиями на педаль тормоза.

3 Продолжить движение с малой скоростью без притормаживания.

После проезда водной преграды необходимо просушить тормозные колодки, выполнив несколько нажатий на тормозную педаль на короткой дистанции пробега.

23. При движении на каком автомобиле увеличение скорости может способствовать устранению заноса задней оси?

1 На переднеприводном.

2 На заднеприводном.

На переднеприводном автомобиле при увеличении скорости ведущие передние колеса будут тянуть за собой задние, тем самым занос будет устранен.
На автомобиле с приводом на задние колеса увеличение скорости только усилит занос задних ведущих колес.

24. Двигаясь в прямом направлении со скоростью 60 км/ч, Вы внезапно попали на небольшой участок скользкой дороги. Что следует предпринять?

1 Плавно затормозить.

2 Не менять траектории и скорости движения.

Небольшой участок скользкой дороги следует преодолевать, не изменяя траектории и скорости движения автомобиля, крепко держась за руль. Это уменьшит вероятность возникновения заноса.

25. Исключает ли антиблокировочная тормозная система возможность возникновения заноса или сноса при прохождении поворота?

1 Полностью исключает возможность возникновения только заноса.

2 Полностью исключает возможность возникновения только сноса.

3 Не исключает возможность возникновения сноса или заноса.

Антиблокировочная система (ABS) предназначена только для предотвращения блокировки колес автомобиля при торможении. Для исключения сноса или заноса ведущих колес при прохождении поворота на современных автомобилях применяют систему систему динамической стабилизации (ESP).

26. Двигаться по глубокому снегу на грунтовой дороге следует:

1 Изменяя скорость движения и передачу в зависимости от состояния дороги.

2 На заранее выбранной пониженной передаче, без резких поворотов и остановок.

Чтобы обеспечить необходимый запас мощности для преодоления больших сил сопротивления, по глубокому снегу на грунтовой дороге следует двигаться на заранее выбранной пониженной передаче, без резких поворотов рулевого колеса и остановки.

27. В каких случаях следует увеличить боковой интервал?

1 При встречном разъезде на большой скорости.

2 При разъезде с длинномерным транспортным средством.

3 При движении по мокрому, скользкому или неровному покрытию.

4 Во всех перечисленных случаях.

В случае встречного разъезда транспортных средств при увеличении скорости должен быть увеличен и боковой интервал между ними для исключения возможного столкновения при внезапном отклонении от траектории движения. При разъезде с длинномерным транспортным средством нужно увеличить боковой интервал, чтобы исключить столкновение с прицепом (полуприцепом), который смещается к центру при поворотах.
При движении по мокрому, скользкому или неровному покрытию требуется увеличение интервала во избежание столкновения.

28. Что подразумевается под временем реакции водителя?

1 Время с момента обнаружения водителем опасности до полной остановки транспортного средства.

2 Время с момента обнаружения водителем опасности до начала принятия мер по ее избежанию.

3 Время, необходимое для переноса ноги с педали подачи топлива на педаль тормоза.

Под временем реакции водителя подразумевается время с момента обнаружения опасности до начала принятия мер по ее избежанию. В зависимости от эмоционального состояния водителя, усталости, его опыта, сложности обстановки, в которой он находится, это время колеблется от 0,5 до 1,5 секунды.

29. При движении в условиях плохой видимости нужно выбирать скорость, исходя из того, чтобы остановочный путь был:

1 Больше расстояния видимости.

2 Меньше расстояния видимости.

Остановочный путь всегда должен быть меньше расстояния видимости. Это позволит вовремя остановиться, если будет замечено препятствие на дороге.

30. Уменьшение тормозного пути транспортного средства достигается:

1 Торможением с блокировкой колес (юзом).

2 Торможением на грани блокировки способом прерывистого нажатия на педаль тормоза.

Уменьшение тормозного пути достигается торможением на грани блокировки прерывистыми нажатиями на педаль. Блокировки колес допускать нельзя, поскольку заблокированные колеса скользят по дороге, и за счет этого увеличивается тормозной путь.

31. Безопасной дистанцией при движении по сухой дороге на легковом автомобиле можно считать расстояние, которое автомобиль пройдет не менее чем за:

1 1 секунду.

2 2 секунды.

3 3 секунды.

Безопасной дистанцией считается расстояние, которое может проехать автомобиль за время реакции водителя и время срабатывания тормозной системы. Время реакции водителя может колебаться от 0,5 до 1,5 секунд, а время срабатывания тормозной системы может составлять от 0,1 до 0,4 секунд. Отсюда следует, что комфортной дистанцией для легковых автомобилей можно считать расстояние, которое проедет автомобиль за время: 1,5 + 0,4 = 2,0, т. е. не менее 2 секунд.

32. Включение каких внешних световых приборов обеспечит Вам наилучшую видимость дороги при движении ночью во время сильной метели?

1 Противотуманных фар совместно с дальним светом фар.

2 Противотуманных фар совместно с ближним светом фар.

При движении ночью во время сильной метели целесообразно использовать включение противотуманных фар совместно с ближним светом фар. Дальний свет использовать нельзя, поскольку он будет создавать слепящее действие и только ухудшит видимость.

33. В каком из перечисленных случаев водителю следует оценивать обстановку сзади?

1 Только при резком торможении.

2 Только при торможении на дороге с мокрым или скользким покрытием.

3 При любом торможении.

При любом торможении водитель должен контролировать обстановку сзади, поскольку водитель, движущийся сзади, может не среагировать вовремя и произойдет авария.

34. Как воспринимается водителем скорость своего автомобиля при длительном движении по равнинной дороге на большой скорости?

1 Кажется меньше, чем в действительности.

2 Кажется больше, чем в действительности.

3 Восприятие скорости не меняется.

Водитель оценивает скорость своего автомобиля по равнинной дороге, в основном, по скорости перемещения таких объектов, как деревья, дорожные знаки, другие автомобили. Если такие объекты длительное время находятся на удаленном расстоянии, то этот визуальный эффект воспринимается водителем как уменьшение скорости движения самого автомобиля. Поэтому в таких условиях водителю следует чаще смотреть на спидометр.

Характеристики движения. Скорость » ГДЗ (решебник) по физике 7-11 классов

14.1. Заполните пропуски в тексте. «Нас окружают различные тела: одни из них относительно нас движутся, а другие…»

14.2. Прочитайте текст и выполните задание.
Мальчик сел на велосипед и поехал по дороге. Его сестра, сидя на скамейке, наблюдает, как рядом с велосипедом бежит собачка, не отставая и не опережая его, а около скамейки, топчась на месте, ожидает возвращения велосипедиста его друг Петя.

14.3. Рассмотрите рисунок и заполните пропуски в тексте, используя слова, приведенные в скобках. «Страж на лету поймал мошку (в точке А) …»

14.4. Длина обода колеса велосипеда составляет l = 2м. Велосипедист проехал путь, равный s =2 км 800 м. Сколько оборотов вокруг своей оси при этом совершило колесо?

14.5. Мальчик съехал с горы на санках из точки А и остановился в точке С. Траектория его движения АВС, причем АВ = ВС. Определите путь мальчика по данным, указанным на рисунке.

15.1. Заполните пропуски в тексте, используя слова, приведенные в скобках. 

15.2. Велосипедист выехал из города и стал двигаться равномерно по прямой дороге. Впишите в пустые окошки значения расстояния от города, на котором находился велосипедист, в указанные на часах моменты времени.

15.3. Мальчик нес ведро с водой, в котором оказалась дырка. Неожиданно начался дождь. Но мальчик продолжал двигаться прямолинейно и равномерно. На рисунке показано расположение следов от капель на дорожке, по которой шел мальчик. Отметьте крестиком следы, которые остались на дорожке от капель, упавших из ведра.

15.4. На рисунке точками отмечены положения мотоциклиста в разные моменты времени, а числами обозначены пройденные им пути за указанный на секундомере промежуток времени. Нарисуйте секундную стрелку на секундомере так, чтобы в целом рисунок иллюстрировал равномерное движение мотоциклиста.

15.5. По прямому стеблю ползет жучок. На рисунке показано, в какие моменты времени жучок находился в обозначенных точках траектории. Согласно рисунку заполните таблицу и охарактеризуйте движение жучка.

16.1. Заполните пропуски числами, чтобы получились правильные фразы.

16.2. Запишите значения физических величин в указанных единицах, заполнив пропуски недостающими числами.

16.3. Заполните пропуски в тексте. «Путь – это … физическая величина».

16.4. Улитка равномерно проползла по листку бумаги отрезок ОА за 20 с. Длина стороны клетки равна 4 мм. Определите скорость улитки и выразите ее значение в указанных единицах. Покажите на рисунке направление скорости улитки.

16.5. Мальчик ехал на велосипеде первые 30 с со скоростью 4 м/с, потом 20 с – со скоростью 5 м/с. Определите среднюю скорость мальчика.

16.6. Первый пролет лестницы длиной 10 м мальчик пробежал за 2 с, второй пролет такой же длины – со скоростью 2 м/с. Найдите среднюю скорость мальчика.

16.7. Пользуясь графиком зависимости пройденного телом пути s от времени t, заполните таблицу.

16.8. В таблице приведены значения пути s, пройденного телом за различные промежутки времени t. Используя эти данные, постройте график зависимости пути s от времени t. Для этого на координатной плоскости постройте шесть точек и соедините их прямой линией.

16.9. Из леса выбежал заяц, пересек поляну за 8 с и опять скрылся в лесу.
а) Используя график зависимости пути s от времени t в период пребывания зайца на поляне, ответьте на вопросы.

б) Заполните таблицу.

в) Анализируя вид графика и значения скорости зайца на разных участках пути, сделайте правильный вывод, зачеркнув в тексте по одному из выделенных слов.

16.10. Вокруг ромашки кружила бабочка. На графике представлена зависимость расстояния l от бабочки до цветка от времени t. Опишите характер движения бабочки на каждом участке графика и запишите в пустых окошках соответствующую цифру.

17.1. Какой путь преодолеет страус за четверть минуты, если будет перемещаться прямолинейно со скоростью 72 км/ч?

17.2. На рисунке приведены графики зависимости пути от времени для двух птиц.

17.3. Проанализируйте график и заполните пропуски в тексте.

17.4. Страус в течение первых 8 с двигался со скоростью 20 м/с.

17.5. На рисунке приведены графики зависимости пути s от времени t для автомобиля А и мотоцикла М, которые выехали из города в одном направлении по прямой дороге. Анализируя графики, ответьте на вопросы.

а) Одновременно ли стартовали машины?
б) Через какое время после мотоцикла выехал из города автомобиль?
в) На каком расстоянии от города произошла встреча автомобиля и мотоцикла (автомобиль догнал мотоцикл)?
г) Через какое время после начала движения мотоцикла его догнал автомобиль?
д) Через какое время после начала движения автомобиль догнал мотоцикл?
е) Определите скорость мотоцикла.
ж) Определите среднюю скорость автомобиля за 3 ч наблюдения.

Равномерное прямолинейное движение – FIZI4KA

1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.

Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.

2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.

Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.

Если за время ​\( t \)​ тело совершило перемещение ​\( \vec{s} \)​, то скорость его движения ​\( \vec{v} \)​ равна ​\( \vec{v}=\frac{\vec{s}}{t} \)​.

Единица скорости: \( [\,v\,]=\frac{[\,s\,]}{[\,t\,]} \); \( [\,v\,]=\frac{1\,м}{1\,с}=1\frac{м}{с} \). За единицу скорости принимается 1 м/с — скорость такого равномерного движения, при котором тело за 1 с совершает перемещение 1 м.

Зная скорость равномерного движения, можно найти перемещение за любой промежуток времени: \( \vec{s}=\vec{v}t \). Вектор скорости и вектор перемещения направлены в одну сторону — в сторону движения тела.

3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.

Пусть \( \vec{s} \) — перемещение тела (рис. 11). Направим координатную ось ОХ по направлению перемещения. Найдем проекцию перемещения на координатную ось ОХ. На рисунке ​\( x_0 \)​ — координата начальной точки перемещения, ​\( x \)​ — координата конечной точки перемещения. Проекция перемещения равна разности координат конечной и начальной точек: ​\( \vec{s}_x=x-x_0 \)​. С другой стороны, проекция перемещения равна проекции скорости, умноженной на время, т.е. \( \vec{s}_x=\vec{v}_xt \). Откуда ​\( x-x_0=\vec{v}_xt \)​ или \( x=x_0+\vec{v}_xt \). Если начальная координата ​\( x_0 \)​ = 0, то ​\( x=\vec{v}_xt \)​.

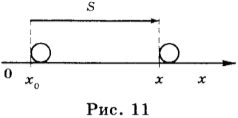
Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.

Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае ​\( x>x_0 \)​. Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае \( x<x_0 \).

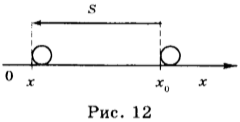
4. Зависимость координаты от времени можно представить графически.

Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: ​\( x \)​ = 4 м/с · ​\( t \)​. Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).

Для того чтобы её построить, необходимо иметь две точки: одна из них ​\( t \)​ = 0 и ​\( x \)​ = 0, а другая ​\( t \)​ = 1 с, ​\( x \)​ = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.

Если в начальный момент времени координата тела ​\( x_0 \)​ = 2 м, а проекция его скорости ​\( v_x \)​ = 4 м/с, то уравнение движения имеет вид: ​\( x \)​ = 2 м + 4 м/с · ​\( t \)​. Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой ​\( t \)​ = 0, ​\( x \)​ = 2 м (рис. 14).

В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \)​ = 2 м – 4 м/с · ​\( t \)​. График зависимости координаты такого движения от времени представлен на рисунке 15.

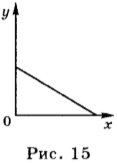
Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.

График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.

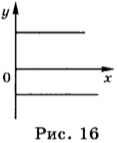
5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.

Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.

При решении задачи целесообразно придерживаться следующей последовательности действий:

1. Кратко записать условие задачи.
2. Проанализировать ситуацию, описанную в условии задачи:
   — выяснить, можно ли принять движущиеся тела за материальные точки;
   — сделать рисунок, изобразив на нём векторы скорости;
   — выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела.
3. Записать в общем виде уравнение движения в векторной форме и для проекций на координатные оси.
4. Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости.
5. Решить задачу в общем виде.
6. Подставить в формулу значения величин и выполнить вычисления.
7. Проанализировать ответ.

Применим эту последовательность действий к приведённой выше задаче.

Дано: ​\( v_1 \)​ = 15 м/с  ​\( v_2 \) ​= 12 м/с  ​\( l \) ​= 270 м. Найти: ​\( t \)​ – ?   \( x\)​ – ?

Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь

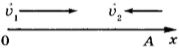
Система отсчёта связана с Землёй, ось ​\( Ox \)​ направлена в сторону движения первого тела, начало отсчёта координаты — т. ​\( O \)​ — положение первого тела в начальный момент времени.

Начальные условия: ​\( t \)​ = 0; ​\( x_{01} \)​ = 0; \( x_{02} \) = 270.

Уравнение в общем виде: ​\( \vec{s}=\vec{v}t \)​; ​\( x=x_0+v_xt \).

Уравнения для каждого тела с учётом начальных условий: ​\( x_1=v_1t \)​; ​\( x_2=l-v_2t \)​. В месте встречи тел ​\( x_1=x_2 \); следовательно: ​\( v_1t=l-v_2t \)​. Откуда ​\( t=\frac{l}{v_1+v_2}\cdot t \)​. Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей: ​\( x \)​ = 150 м.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м
2) 6 м
3) 10 м
4) 150 м

3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — ​\( v_1 \)​ и скорости «Пежо» — \( v_2 \).

1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)

4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости ​\( v_1 \)​ и \( v_2 \).

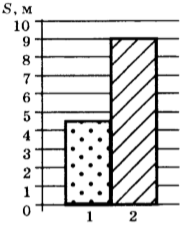
1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

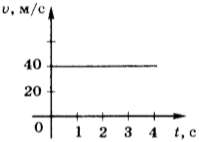
1) 20 м
2) 40 м
3) 80 м
4) 160 м

6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

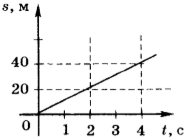
1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с

7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ​\( v_1 \)​, \( v_2 \) и \( v_3 \) движения этих тел.

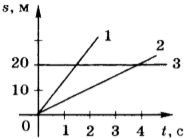
1) ​\( v_1=v_2=v_3 \)​
2) \( v_1>v_2>v_3 \)​
3) \( v_1<v_2<v_3 \)​
4) ​\( v_1=v_2 \), \( v_3<v_1 \)

8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

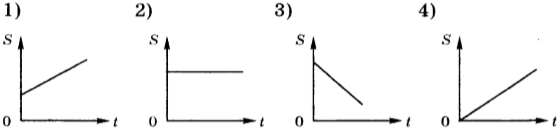
9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

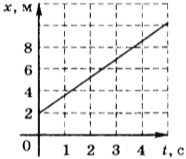
1) 9,8 м
2) 6 м
3) 4 м
4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) ​\( x=1t \)​ (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)

11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

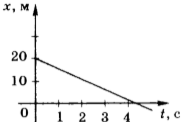
1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Ответы

Равномерное прямолинейное движение

5 (100%) 2 votes